Apollonian gasket
In mathematics, an Apollonian gasket or Apollonian net is a fractal generated from triples of circles, where each circle is tangent to the other two. It is named after Greek mathematician Apollonius of Perga.
Construction
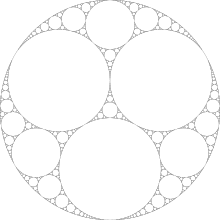
An Apollonian gasket can be constructed as follows. Start with three circles C1, C2 and C3, each one of which is tangent to the other two (in the general construction, these three circles can be any size, as long as they have common tangents). Apollonius discovered that there are two other non-intersecting circles, C4 and C5, which have the property that they are tangent to all three of the original circles – these are called Apollonian circles (see Descartes' theorem). Adding the two Apollonian circles to the original three, we now have five circles.
Take one of the two Apollonian circles – say C4. It is tangent to C1 and C2, so the triplet of circles C4, C1 and C2 has its own two Apollonian circles. We already know one of these – it is C3 – but the other is a new circle C6.
In a similar way we can construct another new circle C7 that is tangent to C4, C2 and C3, and another circle C8 from C4, C3 and C1. This gives us 3 new circles. We can construct another three new circles from C5, giving six new circles altogether. Together with the circles C1 to C5, this gives a total of 11 circles.
Continuing the construction stage by stage in this way, we can add 2·3n new circles at stage n, giving a total of 3n+1 + 2 circles after n stages. In the limit, this set of circles is an Apollonian gasket.
The Apollonian gasket has a Hausdorff dimension of about 1.3057.[1]
Curvature
The curvature of a circle (bend) is defined to be the inverse of its radius.
- Negative curvature indicates that all other circles are internally tangent to that circle. This is bounding circle.
- Zero curvature gives a line (circle with infinite radius).
- Positive curvature indicates that all other circles are externally tangent to that circle. This circle is in the interior of circle with negative curvature.
Variations

An Apollonian gasket can also be constructed by replacing one of the generating circles by a straight line, which can be regarded as a circle passing through the point at infinity.
Alternatively, two of the generating circles may be replaced by parallel straight lines, which can be regarded as being tangent to one another at infinity. In this construction, the circles that are tangent to one of the two straight lines form a family of Ford circles.
The three-dimensional equivalent of the Apollonian gasket is the Apollonian sphere packing.
Symmetries
If two of the original generating circles have the same radius and the third circle has a radius that is two-thirds of this, then the Apollonian gasket has two lines of reflective symmetry; one line is the line joining the centres of the equal circles; the other is their mutual tangent, which passes through the centre of the third circle. These lines are perpendicular to one another, so the Apollonian gasket also has rotational symmetry of degree 2; the symmetry group of this gasket is D2.
If all three of the original generating circles have the same radius then the Apollonian gasket has three lines of reflective symmetry; these lines are the mutual tangents of each pair of circles. Each mutual tangent also passes through the centre of the third circle and the common centre of the first two Apollonian circles. These lines of symmetry are at angles of 60 degrees to one another, so the Apollonian gasket also has rotational symmetry of degree 3; the symmetry group of this gasket is D3.
Links with hyperbolic geometry
The three generating circles, and hence the entire construction, are determined by the location of the three points where they are tangent to one another. Since there is a Möbius transformation which maps any three given points in the plane to any other three points, and since Möbius transformations preserve circles, then there is a Möbius transformation which maps any two Apollonian gaskets to one another.
Möbius transformations are also isometries of the hyperbolic plane, so in hyperbolic geometry all Apollonian gaskets are congruent. In a sense, there is therefore only one Apollonian gasket, up to (hyperbolic) isometry.
The Apollonian gasket is the limit set of a group of Möbius transformations known as a Kleinian group.[2]
Integral Apollonian circle packings
-

Integral Apollonian circle packing defined by circle curvatures of (−1, 2, 2, 3)
-

Integral Apollonian circle packing defined by circle curvatures of (−3, 5, 8, 8)
-

Integral Apollonian circle packing defined by circle curvatures of (−12, 25, 25, 28)
-

Integral Apollonian circle packing defined by circle curvatures of (−6, 10, 15, 19)
-

Integral Apollonian circle packing defined by circle curvatures of (−10, 18, 23, 27)
If any four mutually tangent circles in an Apollonian gasket all have integer curvature then all circles in the gasket will have integer curvature.[3] Since the equation relating curvatures in an Apollonian gasket, integral or not, is
it follows that we may move from one quadruple of curvatures to another by Vieta jumping, just as we do when finding a new Markov number. The first few of these integral Apollonian gaskets are listed in the following table. The table lists the curvatures of the largest circles in the gasket. Only the first three curvatures (of the five displayed in the table) are needed to completely describe each gasket – all other curvatures can be derived from these three.
|
|
Symmetry of integral Apollonian circle packings
No symmetry
If none of the curvatures are repeated within the first five, the gasket contains no symmetry, which is represented by symmetry group C1; the gasket described by curvatures (−10, 18, 23, 27) is an example.
D1 symmetry
Whenever two of the largest five circles in the gasket have the same curvature, that gasket will have D1 symmetry, which corresponds to a reflection along a diameter of the bounding circle, with no rotational symmetry.
D2 symmetry
If two different curvatures are repeated within the first five, the gasket will have D2 symmetry; such a symmetry consists of two reflections (perpendicular to each other) along diameters of the bounding circle, with a two-fold rotational symmetry of 180°. The gasket described by curvatures (−1, 2, 2, 3) is the only Apollonian gasket (up to a scaling factor) to possess D2 symmetry.
D3 symmetry
There are no integer gaskets with D3 symmetry.
If the three circles with smallest positive curvature have the same curvature, the gasket will have D3 symmetry, which corresponds to three reflections along diameters of the bounding circle (spaced 120° apart), along with three-fold rotational symmetry of 120°. In this case the ratio of the curvature of the bounding circle to the three inner circles is . As this ratio is not rational, no integral Apollonian circle packings possess this D3 symmetry, although many packings come close.
Almost-D3 symmetry


The figure at left is an integral Apollonian gasket that appears to have D3 symmetry. The same figure is displayed at right, with labels indicating the curvatures of the interior circles, illustrating that the gasket actually possesses only the D1 symmetry common to many other integral Apollonian gaskets.
The following table lists more of these almost-D3 integral Apollonian gaskets. The sequence has some interesting properties, and the table lists a factorization of the curvatures, along with the multiplier needed to go from the previous set to the current one. The absolute values of the curvatures of the "a" disks obey the recurrence relation a(n) = 4a(n − 1) − a(n − 2) (sequence A001353 in the OEIS), from which it follows that the multiplier converges to
| Curvature | Factors | Multiplier | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a | b | c | d | a | b | d | a | b | c | d | ||
| −1 | 2 | 2 | 3 | 1×1 | 1×2 | 1×3 | N/A | N/A | N/A | N/A | ||
| −4 | 8 | 9 | 9 | 2×2 | 2×4 | 3×3 | 4.000000000 | 4.000000000 | 4.500000000 | 3.000000000 | ||
| −15 | 32 | 32 | 33 | 3×5 | 4×8 | 3×11 | 3.750000000 | 4.000000000 | 3.555555556 | 3.666666667 | ||
| −56 | 120 | 121 | 121 | 8×7 | 8×15 | 11×11 | 3.733333333 | 3.750000000 | 3.781250000 | 3.666666667 | ||
| −209 | 450 | 450 | 451 | 11×19 | 15×30 | 11×41 | 3.732142857 | 3.750000000 | 3.719008264 | 3.727272727 | ||
| −780 | 1680 | 1681 | 1681 | 30×26 | 30×56 | 41×41 | 3.732057416 | 3.733333333 | 3.735555556 | 3.727272727 | ||
| −2911 | 6272 | 6272 | 6273 | 41×71 | 56×112 | 41×153 | 3.732051282 | 3.733333333 | 3.731112433 | 3.731707317 | ||
| −10864 | 23408 | 23409 | 23409 | 112×97 | 112×209 | 153×153 | 3.732050842 | 3.732142857 | 3.732302296 | 3.731707317 | ||
| −40545 | 87362 | 87362 | 87363 | 153×265 | 209×418 | 153×571 | 3.732050810 | 3.732142857 | 3.731983425 | 3.732026144 | ||
Sequential curvatures
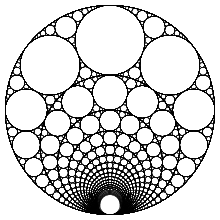
For any integer n > 0, there exists an Apollonian gasket defined by the following curvatures:
(−n, n + 1, n(n + 1), n(n + 1) + 1).
For example, the gaskets defined by (−2, 3, 6, 7), (−3, 4, 12, 13), (−8, 9, 72, 73), and (−9, 10, 90, 91) all follow this pattern. Because every interior circle that is defined by n + 1 can become the bounding circle (defined by −n) in another gasket, these gaskets can be nested. This is demonstrated in the figure at right, which contains these sequential gaskets with n running from 2 through 20.
See also
- Sierpiński triangle
- Apollonian network, a graph derived from finite subsets of the Apollonian gasket
Notes
- ↑ http://abel.math.harvard.edu/~ctm/papers/home/text/papers/dimIII/dimIII.pdf
- ↑ Counting circles and Ergodic theory of Kleinian groups by Hee Oh Brown. University Dec 2009
- ↑ Ronald L. Graham, Jeffrey C. Lagarias, Colin M. Mallows, Alan R. Wilks, and Catherine H. Yan; "Apollonian Circle Packings: Number Theory" J. Number Theory, 100 (2003), 1-45
References
- Benoit B. Mandelbrot: The Fractal Geometry of Nature, W H Freeman, 1982, ISBN 0-7167-1186-9
- Paul D. Bourke: "An Introduction to the Apollony Fractal". Computers and Graphics, Vol 30, Issue 1, January 2006, pages 134–136.
- David Mumford, Caroline Series, David Wright: Indra's Pearls: The Vision of Felix Klein, Cambridge University Press, 2002, ISBN 0-521-35253-3
- Jeffrey C. Lagarias, Colin L. Mallows, Allan R. Wilks: Beyond the Descartes Circle Theorem, The American Mathematical Monthly, Vol. 109, No. 4 (Apr., 2002), pp. 338–361, (arXiv:math.MG/0101066 v1 9 Jan 2001)
External links
| The Wikibook Fractals has a page on the topic of: Apollonian fractals |
- Alexander Bogomolny, Apollonian Gasket, cut-the-knot
- An interactive Apollonian gasket running on pure HTML5 (the link is dead)
- (English) A Matlab script to plot 2D Apollonian gasket with n identical circles using circle inversion
- Online experiments with JSXGraph
- Apollonian Gasket by Michael Screiber, The Wolfram Demonstrations Project.
- Interactive Apollonian Gasket Demonstration of an Apollonian gasket running on Java
- Dana Mackenzie. A Tisket, a Tasket, an Apollonian Gasket. American Scientist, January/February 2010.
- "Sand drawing the world's largest single artwork", The Telegraph, 16 Dec 2009. Newspaper story about an artwork in the form of a partial Apollonian gasket, with an outer circumference of nine miles.