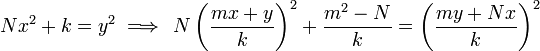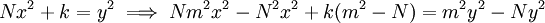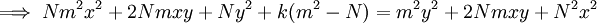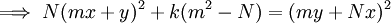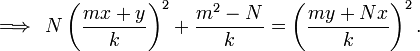Bhaskara's lemma

Bhaskara's Lemma is an identity used as a lemma during the chakravala method. It states that:

\, Nx^2 + k = y^2\implies \,N\left(\frac{mx + y}{k}\right)^2 + \frac{m^2 - N}{k} = \left(\frac{my + Nx}{k}\right)^2

for integers 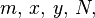$m,\, x,\, y,\, N,$ and non-zero integer $k$ .

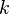Proof

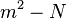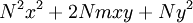The proof follows from simple algebraic manipulations as follows: multiply both sides of the equation by $m^2-N$ , add $N^2x^2+2Nmxy+Ny^2$ , factor, and divide by $k^2$ .

\, Nx^2 + k = y^2\implies Nm^2x^2-N^2x^2+k(m^2-N) = m^2y^2-Ny^2

\implies Nm^2x^2+2Nmxy+Ny^2+k(m^2-N) = m^2y^2+2Nmxy+N^2x^2

\implies N(mx+y)^2+k(m^2-N) = (my+Nx)^2

\implies \,N\left(\frac{mx + y}{k}\right)^2 + \frac{m^2 - N}{k} = \left(\frac{my + Nx}{k}\right)^2.

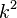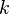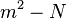So long as neither $k$ nor $m^2-N$ are zero, the implication goes in both directions. (Note also that the lemma holds for real or complex numbers as well as integers.)

References

C. O. Selenius, "Rationale of the chakravala process of Jayadeva and Bhaskara II", Historia Mathematica, 2 (1975), 167-184.
C. O. Selenius, Kettenbruch theoretische Erklarung der zyklischen Methode zur Losung der Bhaskara-Pell-Gleichung, Acta Acad. Abo. Math. Phys. 23 (10) (1963).
George Gheverghese Joseph, The Crest of the Peacock: Non-European Roots of Mathematics (1975).

External links

Introduction to chakravala

Number-theoretic algorithms

Primality tests	AKS test APR test Baillie–PSW Elliptic curve Pocklington Fermat Lucas Lucas–Lehmer Lucas–Lehmer–Riesel Proth's theorem Pépin's Quadratic Frobenius test Solovay–Strassen Miller–Rabin

Prime-generating	Sieve of Atkin Sieve of Eratosthenes Sieve of Sundaram Wheel factorization

Integer factorization	Continued fraction (CFRAC) Dixon's Lenstra elliptic curve (ECM) Euler's Pollard's rho p − 1 p + 1 Quadratic sieve (QS) General number field sieve (GNFS) Special number field sieve (SNFS) Rational sieve Fermat's Shanks' square forms Trial division Shor's

Multiplication	Ancient Egyptian Long Karatsuba Toom–Cook Schönhage–Strassen Fürer's

Discrete logarithm	Baby-step giant-step Pollard rho Pollard kangaroo Pohlig–Hellman Index calculus Function field sieve

Greatest common divisor	Binary Euclidean Extended Euclidean Lehmer's

Modular square root	Cipolla Pocklington's Tonelli–Shanks

Other algorithms	Chakravala Cornacchia LLL Integer square root Modular exponentiation Schoof's

Italics indicate that algorithm is for numbers of special forms

This article is issued from Wikipedia - version of the 6/19/2010. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.