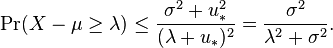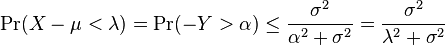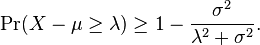Cantelli's inequality
In probability theory, Cantelli's inequality, named after Francesco Paolo Cantelli, is a generalization of Chebyshev's inequality in the case of a single "tail".[1][2][3] The inequality states that
where
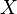 is a real-valued random variable,
is a real-valued random variable,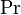 is the probability measure,
is the probability measure,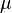 is the expected value of
is the expected value of 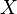 ,
,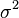 is the variance of
is the variance of 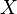 .
.
Combining the cases of 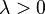 and
and 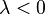 gives, for
gives, for 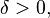
The inequality is due to Francesco Paolo Cantelli. The Chebyshev inequality implies that in any data sample or probability distribution, "nearly all" values are close to the mean in terms of the absolute value of the difference between the points of the data sample and the weighted average of the data sample. The Cantelli inequality (sometimes called the "Chebyshev–Cantelli inequality" or the "one-sided Chebyshev inequality") gives a way of estimating how the points of the data sample are bigger than or smaller than their weighted average without the two tails of the absolute value estimate. The Chebyshev inequality has "higher moments versions" and "vector versions", and so does the Cantelli inequality.
Proof
- Case
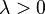 :
:
Let 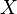 be a real-valued random variable with finite variance
be a real-valued random variable with finite variance 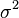 and expectation
and expectation 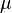 , and define
, and define 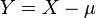 (so that
(so that ![\mathbb{E}[Y] = 0](../I/m/bd2be1291036bea5c101050f798743a2.png) and
and 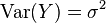 ).
).
Then, for any 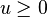 , we have
, we have
the last inequality being a consequence of Markov's inequality. As the above holds for any choice of 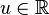 , we can choose to apply it with the value that minimizes the function
, we can choose to apply it with the value that minimizes the function 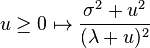 . By differentiating, this can be seen to be
. By differentiating, this can be seen to be 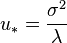 , leading to
, leading to
- Case
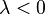 : we proceed as before, writing
: we proceed as before, writing 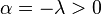 and for any
and for any 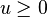
using the previous derivation on 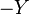 . By taking the complement, we obtain
. By taking the complement, we obtain
References
- ↑ Research and practice in multiple criteria decision making: proceedings of the XIVth International Conference on Multiple Criteria Decision Making (MCDM), Charlottesville, Virginia, USA, June 8–12, 1998, edited by Y.Y. Haimes and R.E. Steuer, Springer, 2000, ISBN 3540672664.
- ↑ "Tail and Concentration Inequalities" by Hung Q. Ngo
- ↑ "Concentration-of-measure inequalities" by Gábor Lugosi
![\Pr(X-\mu\ge\lambda)\quad\begin{cases}
\le \frac{\sigma^2}{\sigma^2 + \lambda^2} & \text{if } \lambda > 0, \\[8pt]
\ge 1 - \frac{\sigma^2}{\sigma^2 + \lambda^2} & \text{if }\lambda < 0.
\end{cases}](../I/m/dd3ddc8d7406153ffd312df284138105.png)
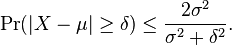
![\Pr( X-\mu \geq\lambda)
= \Pr( Y \geq \lambda)
= \Pr( Y + u \geq \lambda + u)
\leq \Pr( (Y + u)^2 \geq (\lambda + u)^2 )
\leq \frac{\mathbb{E}[(Y + u)^2] }{(\lambda + u)^2}
= \frac{\sigma^2 + u^2 }{(\lambda + u)^2}.](../I/m/8f6cad08e77fd3e2110523f941ac5508.png)