Conical coordinates

Conical coordinates are a three-dimensional orthogonal coordinate system consisting of concentric spheres (described by their radius r) and by two families of perpendicular cones, aligned along the z- and x-axes, respectively.
Basic definitions
The conical coordinates are defined by
with the following limitations on the coordinates
Surfaces of constant r are spheres of that radius centered on the origin
whereas surfaces of constant and are mutually perpendicular cones
and
In this coordinate system, both Laplace's equation and the Helmholtz equation are separable.
Scale factors
The scale factor for the radius r is one (hr = 1), as in spherical coordinates. The scale factors for the two conical coordinates are
and
Alternate Definition
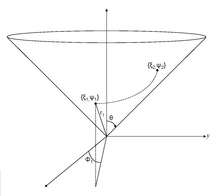
An alternative set of conical coordinates have been derived[1]
where are spherical polar coordinates. The corresponding inverse relations are
The infinitesimal Euclidean distance between two points in these coordinates
If the path between any two points is constrained to surface of the cone given by then the geodesic distance between any two points
and is
References
- ↑ Drake, Samuel Picton; Anderson, Brian D. O.; Yu, Changbin (2009-07-20). "Causal association of electromagnetic signals using the Cayley–Menger determinant". Applied Physics Letters. 95 (3): 034106. doi:10.1063/1.3180815. ISSN 0003-6951.
Bibliography
- Morse PM, Feshbach H (1953). Methods of Theoretical Physics, Part I. New York: McGraw-Hill. p. 659. ISBN 0-07-043316-X. LCCN 52011515.
- Margenau H, Murphy GM (1956). The Mathematics of Physics and Chemistry. New York: D. van Nostrand. pp. 183–184. LCCN 55010911.
- Korn GA, Korn TM (1961). Mathematical Handbook for Scientists and Engineers. New York: McGraw-Hill. p. 179. LCCN 59014456. ASIN B0000CKZX7.
- Sauer R, Szabó I (1967). Mathematische Hilfsmittel des Ingenieurs. New York: Springer Verlag. pp. 991–100. LCCN 67025285.
- Arfken G (1970). Mathematical Methods for Physicists (2nd ed.). Orlando, FL: Academic Press. pp. 118–119. ASIN B000MBRNX4.
- Moon P, Spencer DE (1988). "Conical Coordinates (r, θ, λ)". Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions (corrected 2nd ed., 3rd print ed.). New York: Springer-Verlag. pp. 37–40 (Table 1.09). ISBN 978-0-387-18430-2.