Directed algebraic topology
In mathematics, directed algebraic topology is a refinement of algebraic topology for directed spaces, topological spaces and their combinatorial counterparts equipped with some notion of direction. Some common examples of directed spaces are spacetimes and simplicial sets. The basic goal is to find algebraic invariants that classify directed spaces up to directed analogues of homotopy equivalence. For example, homotopy groups and fundamental n-groupoids of spaces generalize to homotopy monoids and fundamental n-categories of directed spaces. Directed algebraic topology, like algebraic topology, is motivated by the need to describe qualitative properties of complex systems in terms of algebraic properties of state spaces, which are often directed by time. Thus directed algebraic topology finds applications in Concurrency (computer science), Network traffic control, General Relativity, Noncommutative Geometry, Rewriting Theory, and Biological systems.[1]
Directed Spaces
Many mathematical definitions have been proposed to formalise the notion of directed space. E. W. Dijkstra introduced a simple dialect to deal with semaphores, the so-called 'PV language', and to provide each PV program an abstract model: its 'geometric semantics'. Any such model admits a natural partially ordered space (or pospace) structure i.e. a topology and a partial order.[2] The points of the model should be thought of as the states of the program and the partial order as the 'causality' relation between states. Following this approach, the directed paths over the model i.e. the monotonic continuous paths, represent the execution traces of the program. From the computer science point of view, however, the resulting pospaces have a severe drawback. Because partial orders are by definition antisymmetric, their only directed loops i.e. directed paths which end where they start, are the constant loops.
Inspired by smooth manifolds, L. Fajstrup, E. Goubault, and M. Raussen use the sheaf-theoretic approach to define local pospaces.[3] Roughly speaking, a local pospace is a topological space together with an open covering whose elements are endowed with a partial order. Given two elements U and V of the covering, it is required that the partial orders on U and V match on the intersection. Though local pospaces allow directed loops, they form a category whose colimits—when they exist—may be rather ill-behaved.
Noting that the directed paths of a (local) pospace appear as a by-product of the (local) partial order—even though they themselves contain most of the relevant information about direction—Marco Grandis defines d-spaces[4] as topological spaces endowed with a collection of paths, whose members are said to be directed, such that any constant path is directed, the concatenation of two directed paths is still directed, and any subpath of a directed path is directed. D-spaces admit non-constant directed loops and form a category enjoying properties similar to the ones enjoyed by the category of topological spaces.
As shown by Sanjeevi Krishnan, the drawbacks of local pospaces can be avoided if we extend the notion of pospaces by means of 'cosheaves'. The notion of stream[5] is defined thus. More precisely one considers preorders on open subsets and one requires that given any open subset U and any open covering Ω of U, the preorder associated with U is 'generated' by the preorders associated with each member of Ω. The resulting category behaves as nicely as the category of d-spaces. Indeed both of them one can define the directed geometric realization of cubical set (simplicial set) so that its underlying topological space is the (usual) geometric realisation. In fact there is a natural embedding G of the category of streams into the category of d-spaces. This embedding admits a left adjoint functor F. The images of F and G are isomorphic, an isomorphism being obtained by restricting F and G to those images. The category of d-spaces can thus be seen as one of the most general formalisations of the intuitive notion of directed space.
Directed Homotopies between Directed Paths
Regardless of the kind of directed space on considers (pospaces, local pospaces, d-spaces or streams) there is an obvious forgetful functor to the category of topological spaces. Given two directed paths γ and δ, a directed homotopy from γ to δ is a morphism of directed spaces h whose underlying map U(h) is a homotopy –in the usual sense– between the underlying path (topology) U(γ) and U(δ). In algebraic topology, there is a homotopy from α to β if and only if there is a homotopy from β to α. Due to non-reversibility, this is no longer true for directed homotopies. As a consequence, we define the congruence 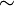 as the least equivalence relation on the directed paths which is compatible with concatenation and relates γ to δ as soon as there is a directed homotopy from γ to δ. Going back to the computer science motivation where directed paths represent execution traces, directed homotopies provide a way to identify execution traces. Hence, given a directed space X which models some concurrent program P, the topology of X can be seen as the 'local commutations' of actions in the program P. In classical models of concurrency like 'asynchronous graphs' of 'Mazurkiewicz traces', the local commutations are provided by a relation over the arrows or the actions.
as the least equivalence relation on the directed paths which is compatible with concatenation and relates γ to δ as soon as there is a directed homotopy from γ to δ. Going back to the computer science motivation where directed paths represent execution traces, directed homotopies provide a way to identify execution traces. Hence, given a directed space X which models some concurrent program P, the topology of X can be seen as the 'local commutations' of actions in the program P. In classical models of concurrency like 'asynchronous graphs' of 'Mazurkiewicz traces', the local commutations are provided by a relation over the arrows or the actions.
The Fundamental Category
The fundamental category of a directed space is defined by mimicking the construction of the fundamental groupoid[6][7] of a topological space. More precisely given a directed space 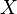 , we consider the (small) category
, we consider the (small) category 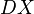 of directed paths over
of directed paths over 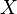 up to monotonic reparametrisation[8] and define the fundamental category of
up to monotonic reparametrisation[8] and define the fundamental category of 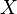 as the quotient
as the quotient 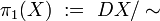 . This construction gives rise to a functor
. This construction gives rise to a functor 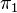 from the category of directed space to the category of small categories.
from the category of directed space to the category of small categories.
Some properties
The fundamental category functor satisfies some kind of Seifert–van Kampen theorem.
The fundamental category functor preserves binary products.
As a consequence of the antisymmetry, the fundamental category C of a pospace is loop-free i.e. for all objects x and y, if both homsets C(x,y) and C(y,x) are nonempty, then x=y and C(x,x) is a singleton.
Two directed paths γ and δ sharing the same image i.e. {γ(t) | t∊dom(γ)} = {δ(t) | t∊dom(δ)} are dihomotopic i.e. γ ~ δ. This property obviously fails in algebraic topology e.g. consider paths winding around the circle.
Given X the model of some concurrent program P, the homsets of the fundamental category of X are countable. In addition, if no looping instruction occurs in P, then the homsets of X are finite. This is the case when P is a PV program in the sense originally given by Dijkstra. In comparison all the nontrivial homsets of the category of directed paths DX are uncountable.
The Category of Components
While the Fundamental Category construction drastically reduces the size of the homsets of DX, it leaves its collection of objects unchanged. And yet, if X is the geometric model of some concurrent program P, this collection is uncountable. The Category of Components was introduced to find a full subcategory of the Fundamental category with as few objects as possible though it contains all the relevant information from the original.[9] If 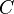 is a loop-free category, then its category of components
is a loop-free category, then its category of components 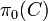 can be described in the language of Category Theory without assuming
can be described in the language of Category Theory without assuming 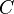 is the fundamental category of some directed space. In this case the intuitive notion of insignificant morphisms is formalised as a collection
is the fundamental category of some directed space. In this case the intuitive notion of insignificant morphisms is formalised as a collection 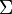 of morphisms of
of morphisms of 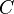 satisfying some stability properties and whose elements both preserve the past of their source and the future of their target. Then
satisfying some stability properties and whose elements both preserve the past of their source and the future of their target. Then 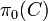 is defined as the quotient[10]
is defined as the quotient[10] 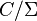 which is proven to be equivalent to the localization of a category
which is proven to be equivalent to the localization of a category ![C[\Sigma^{-1}]](../I/m/b5223487b792c9250b57dceace42b88e.png) .[11] The category of components of a PV program P is then defined as
.[11] The category of components of a PV program P is then defined as 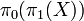 where
where 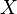 is the geometric model of P. As an interesting property, the category of components of any PV program is finite.
is the geometric model of P. As an interesting property, the category of components of any PV program is finite.
Topics
Higher Order Directed Homotopy
The higher order directed homotopy theory can be developed through cylinder functor and path functor, all constructions and properties being expressed in the setting of categorical algebra![^{[1]}](../I/m/9aa4175f8bbbf1000c08ef6dcb328194.png) . This approach emphasizes the combinatorial role of cubical sets in directed algebraic topology.
. This approach emphasizes the combinatorial role of cubical sets in directed algebraic topology.
The Model Category approach
Philippe Gaucher proposed an alternative formalisation of the notion of directed space which is, roughly speaking, based on the category of directed graphs enriched in topological spaces i.e. the collection of arrows from x to y is endowed with a topology. This approach gives rise to the so-called category of Flows,[12] which admits a nontrivial model category structure. He introduced a topological version (here a topological category means a category equipped with a topological forgetful functor towards the category of sets) using a variant of Marco Grandis' d-spaces, the multipointed d-spaces.[13] In recent papers, he constructed similar model category structures on cubical higher-dimensional transition systems (whose a reflective subcategory is the one of Cattani-Sassone higher-dimensional transition systems) [14] and on labelled symmetric precubical sets.[15] The common points of all these model category structures is 1) the presence of the cofibration {0,1}→{0} identifying two states, 2) the non-contractibility of the directed segment, 3) the strong relationship with the computer-scientific notion of bisimulation. The cylinders of the category of flows and of the category of multipointed d-spaces make the globes oscillate by keeping the set of states constant. All objects of the model categories of flows and multipointed d-spaces are fibrant. It can be checked that the cylinders of these model categories satisfy the homotopy exchange property introduced by Lafont-Métayer-Worytkiewicz in their work about globular omega-categories. The cylinders of the category of cubical transition systems and of labelled symmetric precubical sets make the cubes oscillate by keeping the set of states constant as well. These latter model category structures are constructed using M. Olschok's PhD which generalizes Cisinski's work on the homotopy theory of toposes. In these latter model category structures, all objects are cofibrant.
Thomas Kahl proved the existence of a nontrivial model category of pospaces. Yet this structure barely differs from the model structure over topological spaces. In many regards it just consists of forgetting the partial order of the objects.
Krzysztof Worytkiewicz uses advanced methods from model category theory (namely localization and completion) to build a model category from the small categories of finite-dimensional directed hypercubes.
In fact any attempt to define a model structure over some category of directed spaces has to face the following question: should an inclusion map ![\{*\}\hookrightarrow[0,1]](../I/m/2329f1eddad0b7e16b0ade2952c8ab72.png) be a cofibration, a weak equivalence, both (trivial cofibration) or none. For example, if we suppose
be a cofibration, a weak equivalence, both (trivial cofibration) or none. For example, if we suppose ![\{0\}\hookrightarrow[0,1]](../I/m/851f726a74e5681c8b07a2bd594c9b8f.png) is a trivial cofibration, then
is a trivial cofibration, then ![\{0\}\times[0,1]\cup[0,1]\times\{0\}](../I/m/5ec4e8dc9ce6a0c4e2a570b99b78da56.png) (as a subpospace of the directed plane) is equivalent to a point since the collection of trivial cofibrations is stable under pushout.[16] This fact is prohibitive for computer science application though it is a trivial fact from homotopy theory if we drop the direction feature.
(as a subpospace of the directed plane) is equivalent to a point since the collection of trivial cofibrations is stable under pushout.[16] This fact is prohibitive for computer science application though it is a trivial fact from homotopy theory if we drop the direction feature.
Directed Coverings
...
Software
...
References
- ↑ Directed Algebraic Topology: Models of Non-Reversible Worlds, Marco Grandis, Cambridge University Press, ISBN 978-0-521-76036-2 Free download from authors website
- ↑ Topology and Order. Leopoldo Nachbin, Van Nostrand Company, 1965
- ↑ Algebraic Topology and Concurrency L. Fajstrup, E. Goubault, and M. Raussen, Theoretical Computer Science, 357, 2006, 241-278
- ↑ Directed homotopy theory, I. The fundamental category Marco Grandis, Cahiers Top. Géom. Diff. Catég 44 (2003), 281-316
- ↑ A Convenient Category of Locally Preordered Spaces Sanjeevi Krishnan, 2009, Applied Categorical Structures vol. 17, 5, 445-466
- ↑ Categories and Groupoids, Philip J. Higgins, Van Nostrand Reinhold, 1971
- ↑ Topology and Groupoids. Ronald Brown. Booksurge LLC, 2006
- ↑ Reparametrization of Continuous Paths. Ulrich Fahrenberg and Martin Raussen. Journal of Homotopy and Related Structures, vol. 2(2), 2007, pp.93–117
- ↑ Components of the Fundamental Category. L. Fajstrup, E. Goubault, E. Haucourt, and M. Raussen. App. Cat. Struct. 12(1), 81-108, 2004
- ↑
 Theory and Applications of Categories 5(11) 266–280, 1999
Theory and Applications of Categories 5(11) 266–280, 1999 - ↑ Categories of Components and Loop-Free Categories Emmanuel Haucourt, Theory and Applications of Categories 16(27), 736–770, 2006
- ↑ A model category for the homotopy theory of concurrency P. Gaucher, Homology, Homotopy and Applications, vol. 5 (1):p.549-599, 2003
- ↑ Homotopical interpretation of globular complex by multipointed d-space P. Gaucher, Theory and Applications of Categories, vol. 22, 588-621, 2009
- ↑ Towards a homotopy theory of higher dimensional transition systems P. Gaucher, Theory and Applications of Categories, vol. 25, 295-341, 2011
- ↑ Homotopy Theory of Labelled Symmetric Precubical Sets, P. Gaucher, (preprint ArXiv 2012)
- ↑ Model Categories. Mark Hovey, AMS, 1999
Further reading
- Directed Algebraic Topology and Concurrency, Lisbeth Fajstrup, Éric Goubault, Samuel Mimram, Emmanuel Haucourt, Martin Raussen
- Directed homotopy theory, II. Homotopy Constructs, Marco Grandis, Theory and Applications of Categories, Vol. 10, No. 14, 2002, pp. 369–391
- A Few Points On Directed Algebraic Topology, Marco Grandis
- Directed combinatorial homology and noncommutative tori, Marco Grandis, Math. Proc. Cambridge Philos. Soc. 138 (2005), 233-262