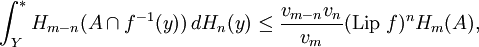Eilenberg's inequality

Eilenberg's inequality is a mathematical inequality for Lipschitz-continuous functions.

Let ƒ : X → Y be a Lipschitz-continuous function between separable metric spaces whose Lipschitz constant is denoted by Lip ƒ. Then, Eilenberg's inequality states that

\int_Y^* H_{m-n}(A\cap f^{-1}(y)) \, dH_n(y) \leq \frac{v_{m-n}v_n}{v_m}(\text{Lip }f)^n H_m(A),

for any A ⊂ X and all 0 ≤ n ≤ m, where

the asterisk denotes the upper Lebesgue integral,
v_n is the volume of the unit ball in Rⁿ,
H_n is the n-dimensional Hausdorff measure.

References

Yu. D. Burago and V. A. Zalgaller, Geometric inequalities. Translated from the Russian by A. B. Sosinskiĭ. Springer-Verlag, Berlin, 1988. ISBN 3-540-13615-0.

This article is issued from Wikipedia - version of the 2/15/2012. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.