Euclid's orchard
In mathematics, informally speaking, Euclid's orchard is an array of one-dimensional "trees" of unit height planted at the lattice points in one quadrant of a square lattice.[1] More formally, Euclid's orchard is the set of line segments from (i, j, 0) to (i, j, 1), where i and j are positive integers.
.svg.png)
.svg.png)
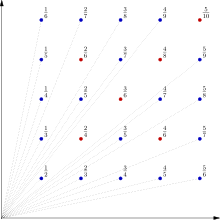
The trees visible from the origin are those at lattice points (m, n, 0), where m and n are coprime, i.e., where the fraction m/n is in reduced form. The name Euclid's orchard is derived from the Euclidean algorithm.
If the orchard is projected relative to the origin onto the plane x + y = 1 (or, equivalently, drawn in perspective from a viewpoint at the origin) the tops of the trees form a graph of Thomae's function. The point (m, n, 1) projects to
See also
References
External links
- Euclid's Orchard, Grade 9-11 activities and problem sheet, Texas Instruments Inc.
- Project Euler related problem