Exeter point

In geometry, the Exeter point is a special point associated with a plane triangle. The Exeter point is a triangle center and is designated as the center X(22)^[1] in Clark Kimberling's Encyclopedia of Triangle Centers. This was discovered in a computers-in-mathematics workshop at Phillips Exeter Academy in 1986.^[2] This is one of the recent triangle centers, having been discovered only in 1986, unlike the classical triangle centers like centroid, incenter, and Steiner point.^[3]

Definition

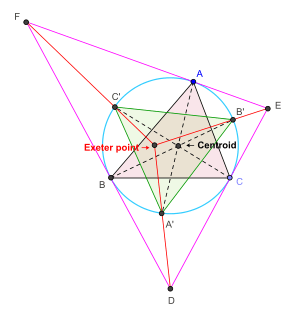
The Exeter point is defined as follows.^[2][4]

Let ABC be any given triangle. Let the medians through the vertices A, B, C meet the circumcircle of triangle ABC at A' , B' and C' respectively. Let DEF be the triangle formed by the tangents at A, B, and C to the circumcircle of triangle ABC. (Let D be the vertex opposite to the side formed by the tangent at the vertex A, E be the vertex opposite to the side formed by the tangent at the vertex B, and F be the vertex opposite to the side formed by the tangent at the vertex C.) The lines through DA' , EB' and FC' are concurrent. The point of concurrence is the Exeter point of triangle ABC.

Trilinear coordinates

The trilinear coordinates of the Exeter point are

( a ( b⁴ + c⁴ − a⁴ ), b ( c⁴ + a⁴ − b⁴ ), c ( a⁴ + b⁴ − c⁴ ) ).

Properties

• The Exeter point of triangle ABC lies on the Euler line (the line passing through the centroid, the orthocenter and the circumcenter) of triangle ABC.

References