Fejér kernel
In mathematics, the Fejér kernel is a summability kernel used to express the effect of Cesàro summation on Fourier series. It is a non-negative kernel, giving rise to an approximate identity. It is named after the Hungarian mathematician Lipót Fejér (1880–1959).
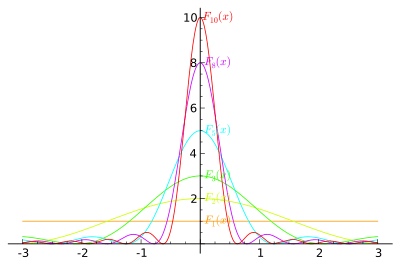
Definition
The Fejér kernel is defined as
where
is the kth order Dirichlet kernel. It can also be written in a closed form as
- ,
where this expression is defined.[1]
The Fejér kernel can also be expressed as
- .
Properties
The Fejér kernel is a positive summability kernel. An important property of the Fejér kernel is with average value of .
Convolution
The convolution Fn is positive: for of period it satisfies
Since , we have , which is Cesàro summation of Fourier series.
- for every
for .
Additionally, if , then
Since is finite, , so the result holds for other spaces, as well.
If is continuous, then the convergence is uniform, yielding a proof of the Weierstrass theorem.
- One consequence of the pointwise a.e. convergence is the uniquess of Fourier coefficients: If with , then a.e. This follows from writing , which depends only on the Fourier coefficients.
- A second consequence is that if exists a.e., then a.e., since Cesàro means converge to the original sequence limit if it exists.