Fodor's lemma

In mathematics, particularly in set theory, Fodor's lemma states the following:

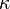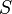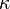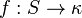If $\kappa$ is a regular, uncountable cardinal, $S$ is a stationary subset of $\kappa$ , and $f:S\rightarrow\kappa$ is regressive (that is, 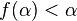$f(\alpha)<\alpha$ for any 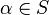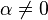$\alpha\in S$ , $\alpha\neq 0$ ) then there is some 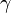$\gamma$ and some stationary 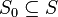$S_0\subseteq S$ such that 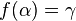$f(\alpha)=\gamma$ for any 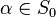$\alpha\in S_0$ . In modern parlance, the nonstationary ideal is normal.

The lemma was first proved by the Hungarian set theorist, Géza Fodor in 1956. It is sometimes also called "The Pressing Down Lemma".

Proof

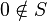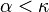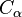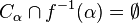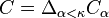We can assume that $0\notin S$ (by removing 0, if necessary). If Fodor's lemma is false, for every $\alpha<\kappa$ there is some club set $C_\alpha$ such that $C_\alpha\cap f^{-1}(\alpha)=\emptyset$ . Let $C=\Delta_{\alpha<\kappa} C_\alpha$ . The club sets are closed under diagonal intersection, so 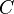$C$ is also club and therefore there is some 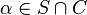$\alpha\in S\cap C$ . 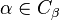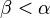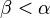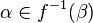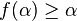Then $\alpha\in C_\beta$ for each $\beta<\alpha$ , and so there can be no $\beta<\alpha$ such that $\alpha\in f^{-1}(\beta)$ , so $f(\alpha)\geq\alpha$ , a contradiction.

Fodor's lemma also holds for Thomas Jech's notion of stationary sets as well as for the general notion of stationary set.

Fodor's lemma for trees

Another related statement, also known as Fodor's lemma (or Pressing-Down-lemma), is the following:

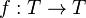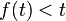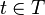For every non-special tree $T$ and regressive mapping $f:T\rightarrow T$ (that is, $f(t)<t$ , with respect to the order on $T$ , for every $t\in T$ ), there is a non-special subtree 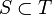$S\subset T$ on which 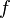$f$ is constant.

References

G. Fodor, Eine Bemerkung zur Theorie der regressiven Funktionen, Acta Sci. Math. Szeged, 17(1956), 139-142.
Karel Hrbacek & Thomas Jech, Introduction to Set Theory, 3rd edition, Chapter 11, Section 3.
Mark Howard, Applications of Fodor's Lemma to Vaught's Conjecture. Ann. Pure and Appl. Logic 42(1): 1-19 (1989).
Simon Thomas, The Automorphism Tower Problem. PostScript file at
S. Todorcevic, Combinatorial dichotomies in set theory. pdf at

This article incorporates material from Fodor's lemma on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

This article is issued from Wikipedia - version of the 12/7/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.