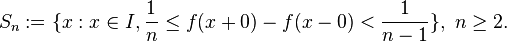Froda's theorem
In mathematics, Darboux-Froda's theorem, named after Alexandru Froda, a Romanian mathematician, describes the set of discontinuities of a monotone real-valued function of a real variable. Usually, this theorem appears in literature without a name. It was written in A. Froda' thesis in 1929 .[1][2]. As it is acknowledged in the thesis, it is in fact due Jean Gaston Darboux [3]
Definitions
- Consider a function f of real variable x with real values defined in a neighborhood of a point
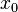 and the function f is discontinuous at the point on the real axis
and the function f is discontinuous at the point on the real axis 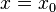 . We will call a removable discontinuity or a jump discontinuity a discontinuity of the first kind.[4]
. We will call a removable discontinuity or a jump discontinuity a discontinuity of the first kind.[4] - Denote
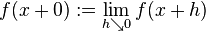 and
and 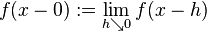 . Then if
. Then if 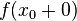 and
and 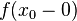 are finite we will call the difference
are finite we will call the difference 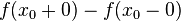 the jump[5] of f at
the jump[5] of f at 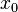 .
.
If the function is continuous at 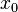 then the jump at
then the jump at 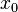 is zero. Moreover, if
is zero. Moreover, if 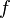 is not continuous at
is not continuous at 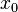 , the jump can be zero at
, the jump can be zero at 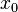 if
if 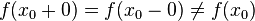 .
.
Precise statement
Let f be a real-valued monotone function defined on an interval I. Then the set of discontinuities of the first kind is at most countable.
One can prove[6][7] that all points of discontinuity of a monotone real-valued function defined on an interval are jump discontinuities and hence, by our definition, of the first kind. With this remark Froda's theorem takes the stronger form:
Let f be a monotone function defined on an interval 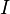 . Then the set of discontinuities is at most countable.
. Then the set of discontinuities is at most countable.
Proof
Let ![I:=[a,b]](../I/m/7f274c91e10afb4aa4e4e31bc0a9e545.png) be an interval and
be an interval and 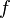 defined on
defined on 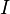 an increasing function. We have
an increasing function. We have
for any 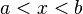 . Let
. Let 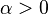 and let
and let 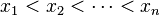 be
be 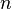 points inside
points inside 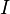 at which the jump of
at which the jump of 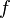 is greater or equal to
is greater or equal to 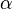 :
:
We have 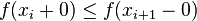 or
or 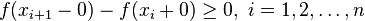 .
Then
.
Then
and hence: 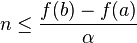 .
.
Since 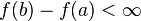 we have that the number of points at which the jump is greater than
we have that the number of points at which the jump is greater than 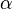 is finite or zero.
is finite or zero.
We define the following sets:
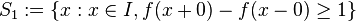 ,
,
We have that each set  is finite or the empty set. The union
is finite or the empty set. The union
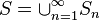 contains all points at which the jump is positive and hence contains all points of discontinuity. Since every
contains all points at which the jump is positive and hence contains all points of discontinuity. Since every 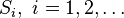 is at most countable, we have that
is at most countable, we have that 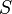 is at most countable.
is at most countable.
If 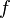 is decreasing the proof is similar.
is decreasing the proof is similar.
If the interval 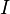 is not closed and bounded (and hence by Heine–Borel theorem not compact) then the interval can be written as a countable union of closed and bounded intervals
is not closed and bounded (and hence by Heine–Borel theorem not compact) then the interval can be written as a countable union of closed and bounded intervals 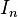 with the property that any two consecutive intervals have an endpoint in common:
with the property that any two consecutive intervals have an endpoint in common: 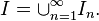
If ![I=(a,b],\ a\geq -\infty \](../I/m/078edaa1a5ec22034aefa57ab5f8842c.png) then
then ![I_1=[\alpha_1,b],\ I_2=[\alpha_2,\alpha_1],\ldots,\ I_n=[\alpha_n,\alpha_{n-1}],\ldots](../I/m/d1da5a2e057d3ba8728dac77d564d6fa.png) where
where 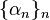 is a strictly decreasing sequence such that
is a strictly decreasing sequence such that 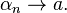 In a similar way if
In a similar way if 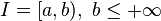 or if
or if 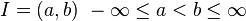 .
.
In any interval 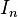 we have at most countable many points of discontinuity, and since a countable union of at most countable sets is at most countable, it follows that the set of all discontinuities is at most countable.
we have at most countable many points of discontinuity, and since a countable union of at most countable sets is at most countable, it follows that the set of all discontinuities is at most countable.
See also
Notes
- ↑ Alexandru Froda, Sur la Distribution des Propriétés de Voisinage des Fonctions de Variables Réelles, These, Harmann, Paris, 3 December 1929
- ↑ Alexandru Froda – Collected Papers (Opera Matematica), Vol.1, Ed. Academ. Romane, 2000
- ↑ Jean Gaston Darboux Mémoire sur les fonctions discontinues, Annales de l'École Normale supérieure, 2-ème série, t. IV, 1875, Chap VI.
- ↑ Walter Rudin, Principles of Mathematical Analysis, McGraw-Hill 1964, (Def. 4.26, pp. 81–82)
- ↑ M. Nicolescu, N. Dinculeanu, S. Marcus, Mathematical Analysis (Bucharest 1971), Vol.1, Pg.213, [in Romanian]
- ↑ W. Rudin, Principles of Mathematical Analysis, McGraw–Hill 1964 (Corollary, p.83)
- ↑ M. Nicolescu, N. Dinculeanu, S. Marcus, Mathematical Analysis (Bucharest 1971), Vol.1, Pg.213, [in Romanian]
References
- Bernard R. Gelbaum, John M. H. Olmsted, Counterexamples in Analysis, Holden–Day, Inc., 1964. (18. Page 28)
- John M. H. Olmsted, Real Variables, Appleton–Century–Crofts, Inc., New York (1956), (Page 59, Ex. 29).
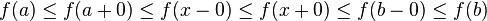
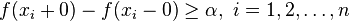
![f(b)-f(a)\geq f(x_n+0)-f(x_1-0)=\sum_{i=1}^n [f(x_i+0)-f(x_i-0)]+](../I/m/d47a13f7cd2f90daa5581631fe84c439.png)
![+\sum_{i=1}^{n-1}[f(x_{i+1}-0)-f(x_i+0)]\geq \sum_{i=1}^n[f(x_i+0)-f(x_i-0)]\geq n\alpha](../I/m/ef444a079af94ed0d542dd4d3f62c553.png)