Gauss–Hermite quadrature

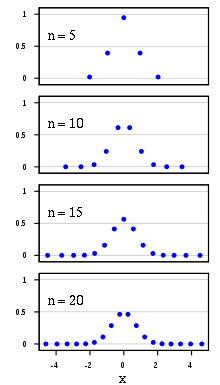
Weights versus x_i for four choices of n

In numerical analysis, Gauss–Hermite quadrature is a form of Gaussian quadrature for approximating the value of integrals of the following kind:

\int _{-\infty }^{+\infty }e^{-x^{2}}f(x)\,dx.

In this case

\int _{-\infty }^{+\infty }e^{-x^{2}}f(x)\,dx\approx \sum _{i=1}^{n}w_{i}f(x_{i})

where n is the number of sample points used. The x_i are the roots of the physicists' version of the Hermite polynomial H_n(x) (i = 1,2,...,n), and the associated weights w_i are given by ^[1]

w_{i}={\frac {2^{n-1}n!{\sqrt {\pi }}}{n^{2}[H_{n-1}(x_{i})]^{2}}}.

Example with change of variable

Let's consider a function h(y), where the variable y is Normally distributed: $y\sim {\mathcal {N}}(\mu ,\sigma ^{2})$ . The expectation of h corresponds to the following integral:

$E[h(y)]=\int _{-\infty }^{+\infty }{\frac {1}{\sigma {\sqrt {2\pi }}}}\exp \left(-{\frac {(y-\mu )^{2}}{2\sigma ^{2}}}\right)h(y)dy$

As this doesn't exactly correspond to the Hermite polynomial, we need to change variables:

$x={\frac {y-\mu }{{\sqrt {2}}\sigma }}\Leftrightarrow y={\sqrt {2}}\sigma x+\mu$

Coupled with the integration by substitution, we obtain:

$E[h(y)]=\int _{-\infty }^{+\infty }{\frac {1}{\sqrt {\pi }}}\exp(-x^{2})h({\sqrt {2}}\sigma x+\mu )dx$

leading to:

$E[h(y)]\approx {\frac {1}{\sqrt {\pi }}}\sum _{i=1}^{n}w_{i}h({\sqrt {2}}\sigma x_{i}+\mu )$

References

↑ Abramowitz, M & Stegun, I A, Handbook of Mathematical Functions, 10th printing with corrections (1972), Dover, ISBN 978-0-486-61272-0. Equation 25.4.46.

Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W., eds. (2010), § 3.5 "Quadrature: Gauss–Hermite Formula" Check |contribution-url= value (help), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR 2723248
Shao, T. S.; Chen, T. C.; Frank, R. M. (1964). "Tables of zeros and Gaussian weights of certain associated Laguerre polynomials and the related generalized Hermite polynomials". Math. Comp. 18 (88): 598–616. doi:10.1090/S0025-5718-1964-0166397-1. MR 0166397.
Steen, N. M.; Byrne, G. D.; Gelbard, E. M. (1969). "Gaussian quadratures for the integrals $\textstyle \int _{0}^{\infty }e^{-x^{2}}f(x)dx$ and $\textstyle \int _{0}^{b}e^{-x^{2}}f(x)dx$ ". Math. Comp. 23 (107): 661–671. doi:10.1090/S0025-5718-1969-0247744-3. MR 0247744.
Shizgal, B. (1981). "A Gaussian quadrature procedure for use in the solution of the Boltzmann equation and related problems". J. Comp. Phys. 41: 309–328. doi:10.1016/0021-9991(81)90099-1.

External links

For tables of Gauss-Hermite abscissae and weights up to order n = 32 see http://www.efunda.com/math/num_integration/findgausshermite.cfm.
Generalized Gauss–Hermite quadrature, free software in C++, Fortran, and Matlab

This article is issued from Wikipedia - version of the 10/14/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.