Sun path

Solar altitude over a year; latitude on northern hemisphere

Sun path polar chart for any location at the latitude of Rotterdam

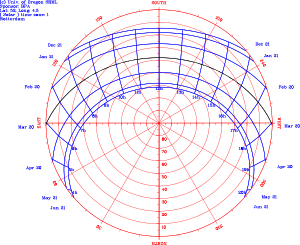
Sun path refers to the apparent significant seasonal-and-hourly positional changes of the sun (and length of daylight) as the Earth rotates, and orbits around the sun. The relative position of the sun is a major factor in the heat gain of buildings and in the performance of solar energy systems.^[1] Accurate location-specific knowledge of sun path and climatic conditions is essential for economic decisions about solar collector area, orientation, landscaping, summer shading, and the cost-effective use of solar trackers.^[2]^[3]

Effect of the Earth's axis tilt

Sun paths at any latitude and any time of the year can be determined from basic geometry.^[4] The Earth's axis of rotation tilts about 23.5 degrees, relative to the plane of Earth's solar system orbit around the Sun. As the Earth orbits the Sun, this creates the 47-degree peak-to-peak solar altitude angle difference, and the hemisphere-specific difference between summer and winter.

In the Northern Hemisphere, the winter sun (December, January, February) rises in the southeast, peaks out at a low angle in the south (more than halfway up from the horizon in the tropics), and then sets in the southwest. It is on the south (equator) side of the house all day long. Vertical south-facing (equator side) window is excellent for capturing solar thermal energy. For comparison, the winter sun in the Southern Hemisphere (June, July, August) rises in the northeast, peaks out at a low angle in the north (more than halfway up from the horizon in the tropics), and then sets in the northwest. There, the north-facing window would let in plenty of solar thermal energy to the house.

In the Northern Hemisphere in summer (June, July, August), the Sun rises in the northeast, peaks out slightly south of overhead point (lower in the south at higher latitude), and then sets in the northwest, whereas in the Southern Hemisphere in summer (December, January, February), the Sun rises in the southeast, peaks out slightly north of overhead point (lower in the north at higher latitude), and then sets in the southwest. A simple latitude-dependent equator-side overhang can easily be designed to block 100% of the direct solar gain from entering vertical equator-facing windows on the hottest days of the year. Roll-down exterior shade screens, interior translucent-or-opaque window quilts, drapes, shutters, movable trellises, etc. can be used for hourly, daily or seasonal sun and heat transfer control (without any active electrical air conditioning).

Everywhere around the world during the equinoxes (March 20/21 and September 22/23) except for the poles, the sun rises due east and sets due west. In the Northern Hemisphere, the equinox sun peaks in the southern half (about halfway up from the horizon at mid latitude) of the sky, while in the Southern Hemisphere, that sun peaks in the northern half of the sky. When facing the equator, the sun appears to move from left to right in the Northern Hemisphere and from right to left in the Southern Hemisphere.

The latitude (and hemisphere)-specific solar path differences are critical to effective passive solar building design. They are essential data for optimal window and overhang seasonal design. Solar designers must know the precise solar path angles for each location they design for, and how they compare to place-based seasonal heating and cooling requirements.

In the U.S., the precise location-specific altitude-and-azimuth seasonal solar path numbers are available from NOAA – the "equator side" of a building is south in the Northern Hemisphere, and north in the Southern Hemisphere, where the peak summer solstice solar altitude occurs on December 21.

On the equator, the sun will be straight overhead and a vertical stick will cast no shadow at solar noon on the equinoxes. On the vernal equinox, north of the subsolar point (on the equator) the vertical stick's shadow will point a little westwards of true north (NNW) reading 336.5° from true north and little eastwards of true south (SSE) reading 156.5° from true north. On the autumnal equinox, north of the subsolar point (on the equator), the shadow will point a little eastwards of true north (NNE) reading 23.5° from true north (and south of the subsolar, the shadow will point a little westward of true south (SSW) reading 203.5° from true north).

The same stick will cast no shadow on the summer solstice in the Northern Hemisphere when the subsolar point is on the Tropic of Cancer 23.44° north of equator. Although north of 23.44°N the shadow will point towards true north and south of 23.44°N the shadow will point towards true south. The reverse occurs on the winter solstice in the Northern Hemisphere when the subsolar point will be on the Tropic of Capricorn 23.44°S and a vertical stick will cast no shadow along that point. But north of the Tropic of Capricorn solar noon shadows will point towards true north and south of the Tropic of Capricorn shadows will point towards true south.

The solar noon shadows of objects on points beyond and below subsolar points will point towards true north and true south respectively only when the solar declination has its maximum positive (δ☉ = +23.44°) or maximum negative (δ☉ = −23.44°) value. On the other hand, on the equinoxes when the sun is neither declined north nor south (δ☉ = 0°) and solar time noon shadows point NNW north of the equator and SSE south of the equator on the vernal equinox (and point NNE north of the equator and SSW south of the equator on the autumnal equinox).

North of the Arctic circle and south of the Antarctic circle, there will be at least one day a year when the sun is not above the horizon for 24 hours during the winter solstice, and at least one day when the sun is above the horizon for 24 hours during the summer solstice.

In the moderate latitudes (between the circles and tropics, where most humans live), the length of the day, solar altitude and azimuth vary from one day to the next, and from season to season. The difference between the length of a long summer day and a short winter day increases as one moves farther away from the equator.^[2]

A solargraph showing the path of the sun as seen in Budapest for every day in 2014. Photo credit: Elekes Andor

Building design simulation

Before the days of modern, inexpensive, 3D computer graphics, a heliodon (precisely-movable light source) was used to show the angle of the sun on a physical model of a proposed building. Today, mathematical computer models calculate location-specific solar gain (shading) and seasonal thermal performance, with the ability to rotate and animate a 3D color graphic model of a proposed building design.

Heating and cooling issues in passive solar building design can be counterintuitive. Precise performance calculations and simulations are essential to avoid reinventing the wheel and duplicating expensive experimental design errors, such as skylights that turn a building into a solar furnace in summer (see Daylighting#Sawtooth roof).

Visualization

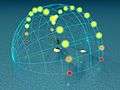
These pictures show such a perspective as follows. They show the day arcs of the Sun, the paths the Sun tracks along the celestial dome in its diurnal movement. The pictures show this for every hour on both solstice days. The longer arc is always the summer track and the shorter one the winter track. The two tracks are at a distance of 46.88° (2 × 23.44°) away from each other.

In addition, some "ghost" suns are indicated below the horizon, as much as 18° down. The Sun in this area causes twilight. The pictures can be used for both the northern and southern hemispheres. The observer is supposed to sit near the tree on the island in the middle of the ocean. The green arrows give the cardinal directions.

On the northern hemisphere the north is to the left, the Sun rises in the east (far arrow), culminates in the south (to the right) while moving to the right and sets in the west (near arrow). Both rise and set positions are displaced towards the north in summer, and towards the south for the winter track.
On the southern hemisphere the south is to the left, the Sun rises in the east (near arrow), culminates in the north (to the right) while moving to the left and sets in the west (far arrow). Both rise and set positions are displaced towards the south in summer, and towards the north for the winter track.

The following special cases are depicted.

On the imaginary line of the equator the Sun maximum elevation is great during all the year but obviously it doesn't form every day a perfect right angle with the ground at noon. In fact it happens two days of the year, during the equinoxes. The solstices are the dates that the Sun stays farthest away from the zenith but anyway also in those cases it's high in the sky, reaching an altitude of 66.56° either to the north or the south. All days of the year, solstices included, have the same length of 12 hours.
The day arcs at 20° latitude. The Sun culminates at 46.56° altitude in winter and 93.44° altitude in summer. In this case an angle larger than 90° means that the culmination takes place at an altitude of 86.56° in the opposite cardinal direction. For example, in the southern hemisphere, the Sun remains in the north during winter, but can reach over the zenith to the south in midsummer. Summer days are longer than winter days, but approximately the difference is no more than only two and a half hours. The daily path of the Sun is steep at the horizon the whole year round, resulting in a twilight of only about one hour and 20 minutes in the morning and in the evening.
The day arcs at 50° latitude. During the winter solstice Sun does not rise more than 16.56° above the horizon at midday, but 63.44° in summer solstice above the same horizon direction. The difference in the length of the day between summer and winter, from here to the north, begin to be striking – slightly more than 8 hours at winter solstice, to more than 16 hours during the summer solstice. Likewise is the difference in direction of sunrise and sunset. At this latitude at midnight (around 1 a.m. with summer legal hour) the summer sun is 16.56° below the horizon, which means that astronomical twilight continues the whole night. This phenomenon is known as the grey nights, nights when it does not get dark enough for astronomers to do their observations of the deep sky. Above 60° latitude the Sun would be even closer to the horizon, only 6.56° away from it. Then civil twilight continues almost all night, only a little bit of "nautical twilight" obviously around the local midnight. This phenomenon is known as the white nights. And above 66.56° latitude, there is no sunset at all, a phenomenon referred to as the midnight sun.
The day arcs at 70° latitude. At local noon the winter Sun culminates at −3.44°, and the summer Sun at 43.44°. Said another way, during the winter the Sun does not rise above the horizon, it is the polar night. There will be still a strong twilight though. At local midnight the summer Sun culminates at 3.44°, said another way, it does not set, it is the polar day.
The day arcs at the pole. At the time of the summer or winter solstices, the Sun is 23.44° degrees above or below the horizon respectively, irrespective of time of day. Whilst the Sun is up (during summer months) it will circle around the whole sky (clockwise from the North Pole and counter-clockwise from the South Pole), appearing to stay at the same angle from the horizon, therefore the concept of day or night is meaningless. The angle of elevation will gradually change on an annual cycle, with the Sun reaching its highest point at the summer solstice, and rising or setting at the equinox, with extended periods of twilight lasting several days after the autumn equinox and before the spring equinox.

Day arcs at 0° latitude, equator.
Day arcs at 20° latitude.
Day arcs at 50° latitude.
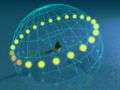
Day arcs at 70° latitude.
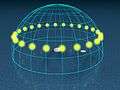
Day arcs at 90° latitude, pole.

References

↑ "Solar Resource Information". National Renewable Energy Laboratory. Retrieved 2009-03-28.
1 2 Khavrus, V.; Shelevytsky, I. (2010). "Introduction to solar motion geometry on the basis of a simple model". Physics Education. 45 (6): 641. doi:10.1088/0031-9120/45/6/010.
↑ Khavrus, V.; Shelevytsky, I. (2012). "Geometry and the physics of seasons". Physics Education. 47 (6): 680. doi:10.1088/0031-9120/47/6/680.
↑ Librorum, Helluo (2012). "Notes from Noosphere: The simple geometry of sun, moon, and star paths". notesfromnoosphere.blogspot.com. Retrieved September 19, 2013.

External links

This article is issued from Wikipedia - version of the 11/10/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.