Geroch's splitting theorem
In the theory of causal structure on Lorentzian manifolds, Geroch's theorem or Geroch's splitting theorem (first proved by Robert Geroch) gives a topological characterization of globally hyperbolic spacetimes.
The theorem
Let 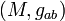 be a globally hyperbolic spacetime. Then
be a globally hyperbolic spacetime. Then 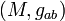 is strongly causal and there exists a global "time function" on the manifold, i.e. a continuous, surjective map
is strongly causal and there exists a global "time function" on the manifold, i.e. a continuous, surjective map 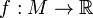 such that:
such that:
- For all
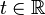 ,
, 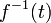 is a Cauchy surface, and
is a Cauchy surface, and 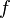 is strictly increasing on any causal curve.
is strictly increasing on any causal curve.
Moreover, all Cauchy surfaces are homeomorphic, and 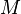 is homeomorphic to
is homeomorphic to 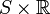 where
where 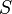 is any Cauchy surface of
is any Cauchy surface of 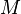 .
.
This article is issued from Wikipedia - version of the 8/17/2012. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.