Hamming scheme
The Hamming scheme, named after Richard Hamming, is also known as the hyper-cubic association scheme, and it is the most important example for coding theory.[1][2][3] In this scheme 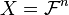 , the set of binary vectors of length
, the set of binary vectors of length 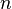 , and two vectors
, and two vectors 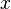 ,
,  are
are 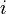 -th associates if they are Hamming distance
-th associates if they are Hamming distance 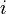 apart.
apart.
Recall that an association scheme is visualized as a complete graph with labeled edges. The graph has 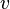 vertices, one for each point of
vertices, one for each point of 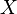 , and the edge joining vertices
, and the edge joining vertices 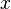 and
and 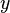 is labeled
is labeled 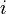 if
if 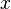 and
and 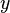 are
are 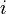 -th associates. Each edge has a unique label, and the number of triangles with a fixed base labeled
-th associates. Each edge has a unique label, and the number of triangles with a fixed base labeled 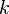 having the other edges labeled
having the other edges labeled 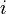 and
and  is a constant
is a constant 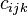 , depending on
, depending on 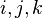 but not on the choice of the base. In particular, each vertex is incident with exactly
but not on the choice of the base. In particular, each vertex is incident with exactly 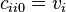 edges labeled
edges labeled 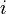 ;
; 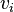 is the valency of the relation
is the valency of the relation 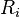 .
The
.
The 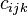 in a Hamming scheme are given by
in a Hamming scheme are given by
Here, 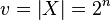 and
and 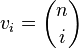 . The matrices in the Bose-Mesner algebra are
. The matrices in the Bose-Mesner algebra are 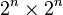 matrices, with rows and columns labeled by vectors
matrices, with rows and columns labeled by vectors 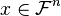 . In particular the
. In particular the 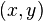 -th entry of
-th entry of 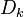 is
is  if and only if
if and only if
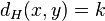 .
.
References
- ↑ P. Delsarte and V. I. Levenshtein, “Association schemes and coding theory,“ IEEE Trans. Inform. Theory, vol. 44, no. 6, pp. 2477–2504, 1998.
- ↑ P. Camion, "Codes and Association Schemes: Basic Properties of Association Schemes Relevant to Coding," in Handbook of Coding Theory, V. S. Pless and W. C. Huffman, Eds., Elsevier, The Netherlands, 1998.
- ↑ F. J. MacWilliams and N. J. A. Sloane, The Theory of Error-Correcting Codes, Elsevier, New York, 1978.
