Harmonious coloring

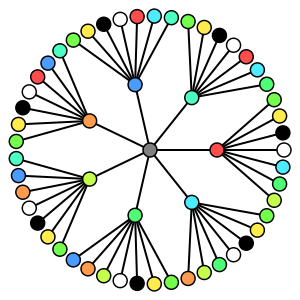
Harmonious coloring of the complete 7-ary tree with 3 levels using 12 colors. The harmonious chromatic number of this graph is 12 since Any fewer colors will result in a color pair appearing on more than one pair of adjacent vertices. Moreover, by Mitchem's Formula, χ_H(T_7,3) = ⌈(3/2)(7+1)⌉ = 12.

In graph theory, a harmonious coloring is a (proper) vertex coloring in which every pair of colors appears on at most one pair of adjacent vertices. The harmonious chromatic number χ_H(G) of a graph G is the minimum number of colors needed for any harmonious coloring of G.

Every graph has a harmonious coloring, since it suffices to assign every vertex a distinct color; thus χ_H(G) ≤ |V(G)|. There trivially exist graphs G with χ_H(G) > χ(G) (where χ is the chromatic number); one example is the path of length 2, which can be 2-colored but has no harmonious coloring with 2 colors.

Some properties of χ_H(G):

1. , where T_k,3 is the complete k-ary tree with 3 levels. (Mitchem 1989)

Harmonious coloring was first proposed by Harary and Plantholt (1982). Still very little is known about it.

See also

• Complete coloring
• Harmonious labeling

External links

• A Bibliography of Harmonious Colourings and Achromatic Number by Keith Edwards

References

• Frank, O.; Harary, F.; Plantholt, M. (1982). "The line-distinguishing chromatic number of a graph". Ars Combin. 14: 241–252. 
• Jensen, Tommy R.; Toft, Bjarne (1995). Graph coloring problems. New York: Wiley-Interscience. ISBN 0-471-02865-7.
• Mitchem, J. (1989). "On the harmonious chromatic number of a graph". Discrete Math. 74: 151–157. doi:10.1016/0012-365X(89)90207-0.