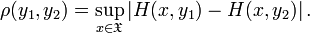Helly metric
In game theory, the Helly metric is used to assess the distance between two strategies. It is named for Eduard Helly.
Consider a game  , between player I and II. Here,
, between player I and II. Here, 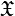 and
and 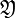 are the sets of pure strategies for players I and II respectively; and
are the sets of pure strategies for players I and II respectively; and  is the payoff function.
is the payoff function.
(in other words, if player I plays 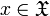 and player II plays
and player II plays 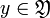 , then player I pays
, then player I pays 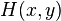 to player II).
to player II).
The Helly metric 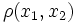 is defined as
is defined as
The metric so defined is symmetric, reflexive, and satisfies the triangle inequality.
The Helly metric measures distances between strategies, not in terms of the differences between the strategies themselves, but in terms of the consequences of the strategies. Two strategies are distant if their payoffs are different. Note that 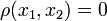 does not imply
does not imply  but it does imply that the consequences of
but it does imply that the consequences of 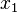 and
and 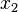 are identical; and indeed this induces an equivalence relation.
are identical; and indeed this induces an equivalence relation.
If one stipulates that 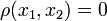 implies
implies  then the topology so induced is called the natural topology.
then the topology so induced is called the natural topology.
The metric on the space of player II's strategies is analogous:
Note that 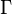 thus defines two Helly metrics: one for each player's strategy space.
thus defines two Helly metrics: one for each player's strategy space.
Conditional compactness
Notation (definition of an  -net). A set
-net). A set 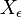 is an
is an  -net in the space
-net in the space 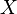 with metric
with metric 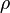 if for any
if for any 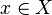 there exists
there exists 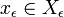 with
with 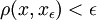 .
.
A metric space 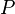 is conditionally compact if for any
is conditionally compact if for any 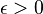 there exists a finite
there exists a finite  -net in
-net in 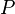 .
.
A game that is conditionally compact in the Helly metric has an  -optimal strategy for any
-optimal strategy for any 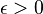 .
.
Other results
If the space of strategies for one player is conditionally compact, then the space of strategies for the other player is conditionally compact (in their Helly metric).
References
N. N. Vorob'ev 1977. Game theory lectures for economists and systems scientists. Springer-Verlag (translated by S. Kotz).