Josephson voltage standard

A Josephson voltage standard is a complex system that uses a superconductive integrated circuit chip operating at 4 K to generate stable voltages that depend only on an applied frequency and fundamental constants. It is an intrinsic standard in the sense that it does not depend on any physical artifact. It is the most accurate method to generate or measure voltage and, by international agreement, is the basis for voltage standards around the World.

The Josephson effect

In 1962, Brian Josephson, a graduate student at Cambridge University, derived equations for the current and voltage across a junction consisting of a thin insulating barrier separating two superconductors – now generally known as a Josephson junction.[1] His equations predicted that if a junction is driven at frequency , then its current-voltage (I-V) curve will develop regions of constant voltage at the values , where is an integer and is the ratio of the Planck constant to the elementary charge . This prediction was verified experimentally by Shapiro [2] in 1963 and has become known as the ac Josephson effect. This effect found immediate application in metrology because it relates the volt to the second through a proportionality involving only fundamental constants. Initially, this led to an improved value of the ratio . Today it is the basis for all primary voltage standards. Josephson's equation for the supercurrent through a superconductive tunnel junction is given by

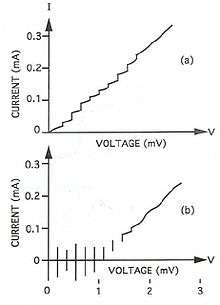
where is the junction current, is the critical current, is the junction voltage. is a function of the junction geometry, the temperature, and any residual magnetic field inside the magnetic shields that are used with voltage standard devices. When a dc voltage is applied across the junction, Eq. (1) shows that the current will oscillate at a frequency , where is approximately equal to 484 GHz/mV. The very high frequency and low level of this oscillation make it difficult to observe directly. However, if an ac current at frequency is applied to the junction, the junction oscillation tends to phase lock to the applied frequency. Under this phase lock, the average voltage across the junction equals . This effect, known as the ac Josephson effect, is observed as a constant voltage step at in the voltage-current (I-V) curve of the junction. It is also possible for the junction to phase lock to harmonics of . This results in a series of steps at voltages , where is an integer, as shown in Fig. 1a.

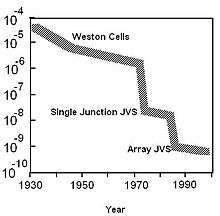
Fig. 1 Constant voltage steps in the I-V curve of a junction driven with microwave radiation for (a) a low capacitance junction and (b) a high capacitance junction.

The Josephson effect was initially used to improve the measurement of the constant based on voltage values derived from the SI volt realization as maintained by Weston cells. The uncertainty of these measurements was limited by the uncertainty of the SI volt realization and the stability of the Weston cells.[3][4] The stability of the Josephson volt depends only on the stability of (which can easily be a part in 1012), and is at least four orders of magnitude better than the stability of Weston cells. Thus, in the early 1970s, many national standards laboratories adopted a value for the Josephson constant and began using the ac Josephson effect as the practical standard of voltage.[5][6] Owing to small differences in existing national standards, different values of were adopted by various countries. This inconsistency was corrected in 1990 when, by international agreement, the constant was assigned the value 483597.9 GHz/V and adopted by all standards laboratories.[7] The assigned value is based on a weighted average of volt realization measurements made prior to 1990 at many national measurement institutions. The uncertainty in is 0.4 ppm. Standards such as the Josephson volt that depend on fundamental constants rather than physical artifacts are known as intrinsic standards. Although the Josephson voltage standard (JVS) does not realize the SI definition of the volt, it provides a very stable reference voltage that can be reproduced anywhere without the need to transfer artifacts such as Weston cells. The accuracy of the Josephson voltage-frequency relation , and its independence from experimental conditions, such as bias current, temperature, and junction materials, have been subjected to many tests.[8][9][10][11][12][13][14][15] No significant deviation from this relation has ever been found. In the most precise of these experiments, two Josephson devices are driven by the same frequency source, biased on the same step, and connected in a series opposition loop across a small inductor. Since this loop is entirely superconductive, any voltage difference leads to a changing magnetic field in the inductor. This field is detected with a SQUID magnetometer and its constancy has set an upper limit on the voltage difference of less than 3 parts in 1019.[16][17] Figure 2 is a semilog plot that illustrates how typical differences in dc voltage measurements among National Measurement Institutes (NMIs) have decreased over the last 70 years.[18][19][20][21][22][23][24] The two major improvements coincide with the introduction of single-junction Josephson standards in the early 1970s and the introduction of series-array Josephson standards beginning in 1984.

Early Josephson standards

Although the ac Josephson effect provides a much more stable voltage reference than Weston cells, the first single-junction Josephson standards [25][26][27][28][29][30][31] were difficult to use because they generated very small voltages (1-10 mV). Several attempts were made to raise the voltage by connecting two or more junctions in series. The most ambitious of these[32] used 20 junctions in series to realize a voltage of 100 mV with an uncertainty of a few parts in 109. Ensuring that every junction was on a constant voltage step required individually adjusting the bias current to each of the 20 junctions. The difficulty of this procedure makes arrays of significantly more than 20 junctions impractical.

Fig. 2 The approximate level of agreement in dc voltage measurements among standards laboratories through the years 1930 to 2000.

In 1977, Levinson et al.[33] made a suggestion that would ultimately lead to a solution to the multiple-bias problem. Levinson pointed out the importance of the parameter in determining the characteristics of rf-induced Josephson steps. is a measure of the damping of Josephson oscillations by the junction shunting resistance. In particular, he showed that junctions with a large capacitance and a large could generate an I-V curve with hysteretic constant-voltage steps like those shown in Fig. 1b. These steps have become known as zero-crossing steps because they cross the zero-current axis of the I-V curve. The lack of stable regions between the first few steps means that for small dc bias currents, the junction voltage must be quantized. With a common bias current at or near zero, the voltage across a large array of these junctions must also be quantized. The possibility of obtaining constant-voltage steps at zero current over a wide range of junction and operating parameters suggested the possibility of building a voltage standard using large arrays of junctions.

After several preliminary experiments,[34][35][36] a joint effort in 1984 between the National Bureau of Standards in the U. S. and the Physikalisch-Technische Bundes-Anstalt in Germany resolved the problems of junction stability and microwave distribution and created the first large Josephson array based on Levinson's idea.[37] Further design improvements and system development produced the first practical 1 V Josephson standards in 1985.[38][39] Advances in superconductive integrated circuit technology, largely driven by the quest for a Josephson junction computer,[40] soon made possible much larger arrays. In 1987, the design was extended to a chip with 14484 junctions that generated about 150 000 quantized voltages spanning the range from -10 V to +10 V.[41] Numerous further refinements were made as 10 V Josephson standards were implemented in many national standards laboratories.[42][43][44][45][46][47][48][49][50][51][52][53][54] By 1989, all of the hardware and software for a complete voltage metrology system was commercially available. Today, there are Josephson array voltage standards in more than 70 national, industrial, and military standards laboratories around the world. A program of international comparisons carried out by the Bureau International des Poids et Mesures (BIPM) has measured differences between a traveling Josephson standard and those of NMI’s that are typically less than 1 part in 109.[55][56]

Junction design details

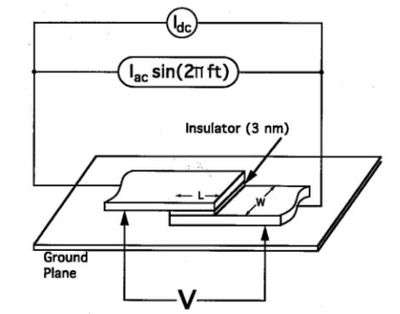
Fig. 3. The structure of a superconductor-insulator-superconductor Josephson junction typically used in dc voltage standards.

Figure 3 illustrates the basic structure of one junction in a large series array. The junction is an overlap between two superconductive thin films that are separated by a thin oxide barrier. The junction sits above a ground plane and is separated from it by a few micrometers of insulation. A dc current and a microwave current are driven through the junction. The design parameters for the junction are its length , width , critical current density (critical current per unit area), and the microwave drive frequency . The practical realization of an array voltage standard requires a thorough understanding of how these parameters affect the stability of the quantized voltage levels shown in Fig. 1b. Stable operation requires that four conditions be satisfied:

  1. must be small enough that the flux induced through the junction area by the microwave magnetic field is much less than the flux quantum
  2. Both and must be small enough that the lowest resonant cavity mode of the junction is greater than
  3. To avoid chaotic behavior, the junction plasma frequency , which is proportional to , must be less than about one third .
  4. The junction's critical current should be as large as possible to prevent noise-induced quantum step transitions.

If any of these conditions is violated, the junction voltage is likely to switch randomly among several steps, making measurements impossible. A rigorous derivation of these conditions is the subject of several papers by Kautz.[57][58]

Fig. 4 A three-dimensional visualization of the region of stable voltage operation as a function of L, W, and J.

Figure 4 illustrates the region of stable behavior in the three-dimensional space of , , and . The margin of stable operation, represented by the shaded volume in Fig. 4, increases with and is ultimately set by a trade-off between stability and the economics of providing a very high frequency microwave source. While stable arrays have been demonstrated at frequencies as low as 24 GHz,[59][60] most practical standards operate in the range 70 – 96 GHz. Table 1 lists a typical set of junction parameters for a commonly used design.

Junction materials Nb/Al2O3/Nb
Critical current density J 20 A/cm2
Junction length L 18 μm
Junction width W 30 μm
Critical current I0 110 μA
Plasma frequency fp 20 GHz
Lowest resonant cavity mode 175 GHz
RF drive frequency f 75 GHz

Table 1 Junction design details

Array Design

The I-V curve shown in Fig. 1b shows steps covering the range from about -1 mV to +1 mV and is for a junction driven by a nearly optimum level of microwave current. At lower microwave current the steps cover a smaller range of voltage and at higher microwave current the steps become smaller and begin to move off the zero current axis. In a large array, every junction must generate a large zero crossing step and thus the microwave power must be adjusted to a value low enough to accommodate the one junction receiving the largest microwave drive. Thus, in order to obtain the largest voltage from the smallest number of junctions, an array standard requires a circuit design that can deliver nearly uniform microwave power to many thousands of junctions, all of which are connected in series. The solution to this problem is a simple extension of Fig. 3 to a series of junctions in a line over a ground plane as shown in Fig. 5a. This results in a microwave stripline that can propagate microwave power with relatively low loss. The capacitive impedance of the junctions is so small (approximately 1 m Ω ) relative to the strip line impedance (approx. 3 Ω) that each junction has a very minor effect on the propagation of microwave power in the strip line. Typically, each junction will absorb about 0.02% to 0.04% of the power propagating through it. It is thus possible to connect several thousand junctions in series and still achieve a power uniformity of about ±1.5 dB. With careful design, striplines with as many as 4800 junctions have been used.[61]

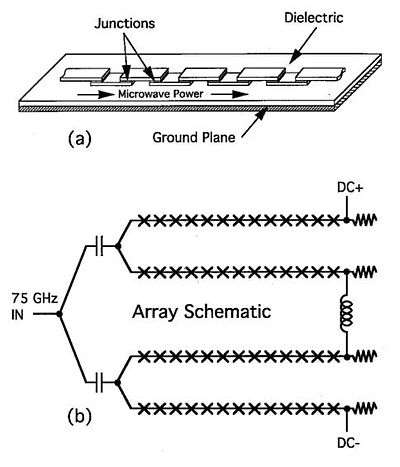
Fig. 5. (a) A series of Josephson junctions arranged to form a stripline and (b) the circuit of a typical Josephson voltage standard integrated circuit chip.

Because 10 V Josephson standards require about 20 000 junctions, it is necessary to adopt a series/parallel circuit similar to that shown in Fig. 5b.[39] Here, a network of low- and high-pass filters allow the microwave power to be split into four parallel paths while maintaining a dc path in which all junctions are connected in series.

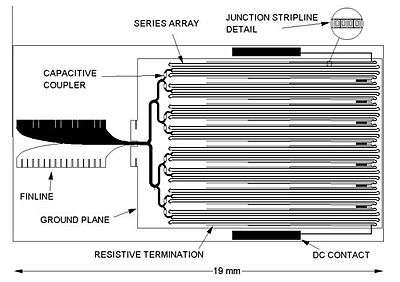
Fig. 6. The layout of a 20 208 junction, 10 V Josephson array voltage standard chip.

A typical integrated circuit layout for an array of 20 208 junctions is shown in Fig. 6. The microwave drive power is collected from a waveguide by a finline antenna, split 16 ways, and injected into 16 junction strip lines of 1263 junctions each. The junction striplines are separated from a superconductive ground plane by about 2 micrometers of SiO2 dielectric. Symmetry in the splitting network ensures that the same power is delivered to each subarray. Several precautions are required to avoid reflections that would lead to standing waves and the consequent nonuniform power distribution within the subarrays: (1) Each stripline is terminated by a matched load that consists of several wavelengths of resistive strip line. The use of resistive stripline rather than a discrete resistor guarantees a near perfect match over a wide range of fabrication parameters. The dimensions of capacitors in the low- and high-pass filters are chosen to avoid resonances near the drive frequency. (3) The microwave bend radius has a minimum value of three times the stripline width. Sharper bends result in unacceptable reflections. In order to meet the bend requirement while still packing the array strips close together, "curly" bends that turn 215° and then back 45° are used. (4) The junction spacing along the line must be close enough to avoid a resonance between adjacent junctions.[62] Microwave power is applied by inserting the finline end of the chip into a slot parallel to the E-field in a WR-12 waveguide. The dc output appears across superconducting pads at the edge of the chip.

Fabrication

Voltage standard chips are typically fabricated on silicon or glass substrates. The integrated circuit has eight levels: (1) a 300 nm thick Nb ground plane, (2) a 2μm layer of SiO2 that forms the microstripline dielectric, (3) a 200 nm Nb film that forms the lower electrode of the Josephson junctions, (4) a 3 nm metal oxide layer that forms the Josephson tunneling barrier, (5) a 100 nm Nb junction counter electrode (6) a 300 nm SiO2 film with windows for contacts to the counter electrode, (7) a 400 nm film of Nb that connects the junction counter electrodes, and (8) a 100 nm resistive film that forms the stripline terminations.

Measurement systems

A block diagram of a modern Josephson voltage standard system is shown in Fig. 7. The Josephson array chip is mounted inside a high-permeability magnetic shield at the end of a cryoprobe that makes the transition between a liquid helium Dewar and the room temperature environment. Some systems use a cryocooler to cool the chip and eliminate the need for liquid helium. Three pairs of copper wires are connected to the array. One pair supplies bias current, a second monitors the array voltage with an oscilloscope, and the third pair delivers the array voltage to the calibration system. All of the wires pass through multiple levels of RFI filtering in a box at the top of the Dewar. The box, the filters, and the Dewar itself form a shield that protects the Josephson array from electromagnetic interference that could cause step transitions. Microwave power is delivered through a waveguide consisting of a 12 mm diameter tube with WR-12 launching horns on each end. Tubes of solid German silver or stainless steel plated internally with silver or gold are commonly used. This waveguide simultaneously achieves low thermal loss (<0.5 L liquid He per day) and low microwave loss (as low as 0.7 dB at 75 GHz).

Fig. 7 Block diagram of a voltage standard system.

A phase-locked oscillator (PLO) operating at a frequency near 75 GHz provides the microwave power to the chip. The primary requirements for the 75 GHz source are: (1) its frequency must be known with high accuracy ( 1 part in 1010 ) and (2) it should produce a stable output power of at least 50 mW. It is useful, although not essential, to be able to tune the source over a range of frequencies. The PLO may be constructed using a commercial microwave counter with feedback capability or it may be a custom built phase-locked loop. More recently microwave frequency synthesizers that are more reliable and offer a wider tuning range and resolution have become the preferred microwave source. The frequency reference for the system is usually a 10 MHz sine wave derived from a GPS receiver or an atomic clock.

The zero crossing steps of Fig. 1b allow a single bias current passing through the entire junction array while insuring that every junction in the array is on a constant voltage step. This leads to significant complication in setting the array to a particular desired step. Figure 9a illustrates a simplified diagram of the bias circuit. In this circuit a computer sets the bias voltage with one digital-to-analog converter (DAC) and uses a second DAC to control the bias impedance via optically modulated resistors. Figure 9b shows a graphical solution for the stable operating points of the array and illustrates how control of both the bias voltage and the bias impedance is used to select a particular quantum voltage step.[63] The load line plots the range of voltage and current that are defined by the bias supply. The intersections of this load line with the I-V curve of the array (vertical lines) are possible stable bias points. Changes to shift the load line left and right, whereas changes to change its slope. To select a step at a given voltage , the source voltage is set to and the source impedance is set to about , where is the step height. This makes the load line steep enough to intersect only one or two steps and forces the array to a step at or very near . Applying a damped oscillation to helps move the array to the step closest to . After a step is selected, the source impedance is smoothly increased on all four bias connections (load line becomes horizontal) until the array current goes to zero and the array is effectively disconnected from the bias source. This open-bias condition is the most stable state for the array and eliminates the possibility of any errors resulting from a small series resistance in the array – a common array defect. Computer control of this three-step process enables the system to find and stabilize the array voltage on a particular step within a few seconds. High quality Josephson arrays will remain on a selected step for many hours.

Fig. 8 (a) The bias circuit for a JVS and (b) a graphical solution of the operating points for the Josephson array.

Numerous algorithms have been developed to compare a Josephson standard with a secondary standard or another Josephson standard. These algorithms differ in the amount of averaging used, the type and placement of reversing switches, and the statistical methods used to reduce the data and compute uncertainty. The selection of an algorithm depends on the type of comparison, the desired level of uncertainty, and the time available. One commonly used algorithm that is appropriate for calibrations of Zener reference standards is described here.

Example measurement algorithm

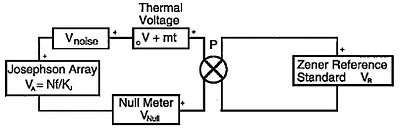
Fig.9 The measurement loop used to determine the voltage of an unknown device relative to the Josephson standard.

The voltage of an unknown reference relative to the Josephson array voltage is determined using the circuit shown in Fig. 9 (a subset of Fig. 7) in which the unknown and the Josephson array are connected in series opposition across a null meter. A reversing switch is used to eliminate the effect of thermal and other offset voltages. The step number and sometimes the frequency are adjusted to make the null voltage as small as possible. The circuit equation can then be written:

Here, is the Josephson array voltage, V0 is a combination of thermal offset voltages and any offset voltage in the nullmeter, mt represents a linear drift component of the offset voltage, is the polarity of the reversing switch, is the differential null voltage, and represents noise in the unknown, the null meter, and any other sources of random noise. Now define a parameter , where is a measurement at time and is determined from using

where is an initial direct measurement of by the system voltmeter and the "Round" function means rounded to the nearest integer. The direct measurement of is obtained by setting the array to the step, which can be seen from Fig. 7 to connect the voltmeter directly to the Zener reference.

Based on measurements of and , a set of values and is acquired for . Three successive values of are examined for consistency within 2 μV before the data are accepted. This eliminates data that may be corrupted by the transient that occurs when there is a spontaneous transition between quantum voltage steps. Since and change by equal amounts during a step transition, remains constant thus making the data collection process relatively immune to step transitions. Data are collected efficiently even for a Josephson array chip that may be making as many as five transitions per minute. The scatter in the data that results from noise in the unknown and in the null meter can generally be modeled by a Gaussian process with one standard deviation on the order of 20 to 100 nV. There are, however, occasional noise spikes that do not fit this process and generate glitches in the data that may lie 1 μV to 10 μV away from the well behaved data. An outlier test is used to detect and eliminate such data.

After the collection of the first data set, the polarity of the unknown is reversed (), the bias is readjusted to select a step that minimizes , and a second set of data is acquired. Two more reversals generate third and fourth data sets. Best estimates for , and are obtained from a least-squares recursion analysis that minimizes the root-sum-square (RSS) error of the set for all in the four data sets. In typical measurements of Zener standards, the noise of the standard often dominates the computed value of . The type A uncertainty for is the standard deviation of the mean for the set of . Typically, this entire calibration algorithm is controlled by a computer and is completed in a few minutes. Except in the case of data with nonuniform delays between the reversals, a simple average of the absolute values of the full set of is an equally good estimate of .

Systems like that shown in Fig. 7 are used to calibrate secondary standards, such as Weston cells, Zener references, and precise digital voltmeters. These calibrations are greatly simplified by the fact that the Josephson array voltage can be set to any value , where the integer can have any value in the range of about -75 000 to +75 000. The typical uncertainty in measurements of 10 V Zener standards is limited by noise in the Zener to about 0.01 ppm. The ability to set the Josephson array to a wide range of discrete voltages also makes it the most accurate tool for measuring the linearity of high-accuracy digital voltmeters.

Uncertainty

While the voltage appearing across the terminals of a Josephson device is, in principle, given exactly by , in any real measurement there are a variety of potential sources of error and uncertainty as listed in Table 2. In the case of a known error, such as a reference frequency offset or a known leakage resistance, a correction can be made. It is then the metrologist’s task to assign realistic numbers to all uncertainties including the uncertainty in the corrections. One method of doing this notes that only items 1 and 2 in Table 2 depend on the voltage across the Josephson array. All of the other components are about the same regardless of the array voltage. Therefore, the combined effect of items 3-8 can be quantitatively evaluated by making a set of measurements of a short circuit using exactly the same algorithm that is used for any other measurement. The standard error resulting from items 3-8 is just the root mean square (RMS) value of the set of short circuit measurements.[64] Additional experiments must be performed to estimate frequency and leakage uncertainty. Internationally accepted procedures for combining uncertainty and establishing confidence intervals is the subject of the BIPM’s Guide to the Evaluation of Uncertainty in Measurement.[65] Typically, the total uncertainty contribution of a Josephson system in a measurement averaging time of a few minutes is a few nanovolts. Since the most common use of these systems is the calibration of Zener standards with a noise level of 50-100 nV, the contribution of the Josephson system is negligible.

1 Reference frequency offset and noise
2 Voltage drops in the measurement loop caused by leakage currents
3 Null meter gain error, bias current, offset, input impedance, nonlinearity, and noise
4 Uncorrected thermal voltages in the measurement loop
5 Offset owing to rectification of the reference frequency current in array defects
6 Any effect of electromagnetic interference
7 Defective junctions or connections leading to a bias dependent voltage
8 The product of series resistance in the array and any residual bias current

Table 2. Potential sources of error and uncertainty for a Josephson standard

Traceability and Equivalence

Josephson junction array chip developed by the National Bureau of Standards as a standard volt

A Congressional act in 1904 established the U.S. Legal Volt to be a quantity defined by the National Bureau of Standards, now the National Institute of Standards and Technology (NIST). With the 1990 international agreement on the Josephson representation of the volt, NIST defined the U.S. Legal Volt to be the same as the international volt representation. Since the success of the first Josephson array voltage standards in 1984, their use has proliferated to more than 70 national measurement institutes (NMI's), military, and commercial laboratories around the world. This has resulted in some confusion about the traceability of non-NMI's that are in possession of a JVS that is, in principle, as good as the national standard. Some guidance on this question is provided in International Standards Organization (ISO) documents that state the general principle that intrinsic standards like the JVS, that have participated in a comparison with an NMI, can claim traceability.

References

  1. ↑ B.D. Josephson, Phys. Lett., 1, 251 (1962)
  2. ↑ S. Shapiro, Phys. Rev. Lett. 11 80 (1963)
  3. ↑ W.H. Parker, D.N. Langenberg, A. Denenstein and B.N. Taylor, Phys. Rev. 177 639 (1969)
  4. ↑ T.F. Finnegan, A. Denenstein and D.N. Langenberg, Phys. Rev. B 4 1487 (1971)
  5. ↑ B.N. Taylor, W.H. Parker, D.N. Langenberg, and A. Denenstein, Metrologia 3 89 (1967)
  6. ↑ B.F. Field, T.F. Finnegan and J. Toots, Metrologia 9 155 (1973)
  7. ↑ T.J. Quinn, Metrologia 26 69 (1989)
  8. ↑ J. Clarke, Phys. Rev. Lett. 21 1566 (1968)
  9. ↑ T. D. Bracken, and W.O. Hamilton, Phys. Rev. B 6 2603 (1972)
  10. ↑ I. K. Harvey, J.C. MacFarlane, and R.B. Frenkel, Metrologia 8 114 (1972)
  11. ↑ F. Bloch, Phys. Rev. Lett. 21 1241 (1968), Phys. Rev. B, 2 109 (1970)
  12. ↑ T. R. Rieger, D. J. Scalapino, and J. E. Mercereau, Phys. Rev. Lett. 27 1787 (1971)
  13. ↑ T. A. Fulton, Phys. Rev. B, 7 981 (1973)
  14. ↑ J. Niemeyer, L. Grimm, C.A. Hamilton, and R. L. Steiner IEEE Electron Dev. Lett. 7 44 (1986)
  15. ↑ V. Kose, and J. Niemeyer: in The Art of Measurement, ed. B. Kramer (Weinheim: VCH) 249 (1988)
  16. ↑ J-S Tsai, A. K. Jain, and J. E. Lukens, Phys. Rev. Lett. 51 316 (1983)
  17. ↑ A.K. Jain, J.E. Lukens, and J.S. Tsai, Phys. Rev. Lett. 58 1165 (1987)
  18. ↑ B. W. Petley: in Quantum Metrology and Fundamental Physical Constants, edited by P.H. Cutler and A. A. Lucas (Plenum, New York) 293 (1983)
  19. ↑ F. Melchert, Tech. Messen 2 59 (1979).
  20. ↑ D. Reymann and T. J. Witt, IEEE Trans. Instrum. Meas. 42 596 (1993).
  21. ↑ J. P. Lo-Hive, D. Reymann and G. Genevès, IEEE Trans. Instrum. Meas. 44 230 (1995)
  22. ↑ D. Reymann, T.J. Witt, G. Eklund, H. Pajander, and H. Nilsson, IEEE Trans. Instrum. Meas. 46 220 (1997)
  23. ↑ D. Reymann, T. J. Witt, G. Eklund, H. Pajander, H. Nilsson, R. Behr, T. Funck and F.Müller, IEEE Trans. Instrum. Meas. 48 257 (1999).
  24. ↑ J. Niemeyer in Handbook of Applied Superconductivity, ed. Bernd Seeber, (Inst. Of Physics Publishing, Philadelphia), 2 p. 1813 (1998)
  25. ↑ F. K. Harris, F. K. Fowler, and P. T. Olsen, Metrologia, 6 134 (1970)
  26. ↑ B.N. Taylor, Low Temperature Physics, LT-13 4,465, (1972)
  27. ↑ W.G. Eicke, T.F. Finnegan, and J. Toots, Metrologia, 9, 155-156, (1973)
  28. ↑ R.F.Dziuba, B.F. Field, and T.F. Finnegan, IEEE Trans. Instrum. Meas. 23 264 (1974)
  29. ↑ B.F. Field and V.W. Hesterman, IEEE Trans Instrum Meas., 25 509 (1976)
  30. ↑ T.F. Finnegan, J. Wilson, and J. Toots, IEEE Trans. Magn., 11 821 (1975)
  31. ↑ T.F. Finnegan, L.B. Holdeman, and S. Wahlsten, IEEE Trans. Magn. 13 392 (1977)
  32. ↑ T. Endo, M. Hoyanagi and A. Nakamura; IEEE Trans. Instrum. Meas., 32 267 (1983)
  33. ↑ M.T. Levinson, R.Y. Chiao, M.J. Feldman and B.A. Tucker, Appl. Phys. Lett., 32 776 (1977)
  34. ↑ R.L. Kautz, Appl. Phys. Lett., 36, 386 (1980)
  35. ↑ R.L. Kautz and G. Costabile, IEEE Trans. Magn., 17 780 (1981)
  36. ↑ J. Niemeyer, J.H. Hinken and W Meier, IEEE Trans. Instrum. Meas. 33, 311 (1984)
  37. ↑ J. Niemeyer, J. H. Hinken and R. L. Kautz, Appl. Phys. Lett. 45 478 (1984); IEEE Trans. Instrum. Meas., 34, 185 (1985)
  38. ↑ C.A. Hamilton, R.L. Kautz, R.L. Steiner and F.L. Lloyd, IEEE Electron Device Lett., 6, 623 (1985)
  39. ↑ [46] J. Niemeyer, L. Grimm, W. Meier, J.H. Hinken and E. Vollmer. Appl. Phys. Lett., 47, 1222 (1985)
  40. ↑ IBM J. Res. and Dev. 24 105 (1980)
  41. ↑ F.L. Lloyd, C.A. Hamilton, J.A. Beall, D. Go, R.H. Ono and R.E. Harris,IEEE Electron Device Lett., 8, 449 (1987)
  42. ↑ C. A. Hamilton, R. L. Kautz, F. L. Lloyd, R. L. Steiner, B. F. Fields, IEEE Trans. Instrum. Meas. 36 258, (1987)
  43. ↑ C.A. Hamilton, F.L. Lloyd, C. Kao and W.C. Goeke, IEEE Trans. Instrum. Meas, 38, 314 (1989)
  44. ↑ R.L. Steiner and B.F. Field, IEEE Trans. Instrum. Meas. 38, 296 (1989)
  45. ↑ R. Pöpel, J. Niemeyer, W Meier L Grimm, F.W. Dünschede, IEEE Trans. Instrum. Meas. 40 298 (1991)
  46. ↑ R. Pöpel, J. Niemeyer, R. Fromknecht, W. Meier, and L. Grimm, J. Appl. Phys. 68 4294 (1990)
  47. ↑ R. Pöpel, Metrologia, 29 153 (1992)
  48. ↑ R.L. Steiner and R.J. Astalos, IEEE Trans. Instrum. Meas. 40 321 (1991)
  49. ↑ R.L. Steiner, A.F. Clark, C. Kiser, T.J. Witt and D. Reymann, IEEE Trans. Appl. Supercond., 3 1874 (1993)
  50. ↑ F. Müller, R. Pöpel, J. Kohlmann, J. Niemeyer, W. Meier, T. Weimann, L. Grimm, F. Dünschede, and P. Gutmann, IEEE Trans. Instrum. Meas. 46 229 (1997)
  51. ↑ C. A. Hamilton, S. L. Kupferman, C. J. Burroughs, G. Naujoks, and A. Vickery, IEEE Trans. Instrum. Meas. 46 237 (1997)
  52. ↑ Y. Murayama, T. Sakuraba, Y. Sakamoto, A. Iwasa, H. Yoshida, T. Kozakai, and T. Endo, IEEE Trans. Instrum. Meas. 46 233 (1997)
  53. ↑ S. L. Kupferman and C. A. Hamilton, IEEE Trans. Instrum. Meas. 48 249 (1999)
  54. ↑ Y. –H. Tang, R. T. Hunt, R. Robertazzi, M. A. Fisher, J. Coughlin, R. Patt, E. K. Track, and E. Potenziani, IEEE Trans. Instrum. Meas. 46 256 (1997)
  55. ↑ D. Reymann and T. J. Witt, IEEE Trans. Instrum. Meas. 42 596 (1993)
  56. ↑ J. P. Lo-Hive, D. Reymann and G. Genevès, IEEE Trans. Instrum. Meas. 44 230 (1995)
  57. ↑ R. L. Kautz, J. Appl. Phys. 76 5538 (1994)
  58. ↑ R. L. Kautz, Rev. Prog. Phys. 59 935 (1996)
  59. ↑ F. Müller, H.-J. Köhler, P. Weber, K. Blüthner and H.-G. Meyer, J. Appl. Phys. 68 4700 (1990)
  60. ↑ C. A. Hamilton, R. L. Kautz, M. Stieg, K. Chieh, W. F. Avrin, and M. B. Simmonds, IEEE Trans. Instrum. Meas. 40 301 (1991)
  61. ↑ F. Müller, R. Pöpel, J. Kohlmann, J. Niemeyer, W. Meier, T. Weimann, L. Grimm, F. Dünschede, and P. Gutmann, IEEE Trans. Instrum. Meas. 46 229 (1997)
  62. ↑ R. L. Kautz, in Metrology at the Frontiers of Physics and Technology, ed. L. Grovini and T. J. Quinn (Amsterdam: North-Holland) 259 (1992)
  63. ↑ C.A. Hamilton, R.L. Kautz, F.L. Lloyd,, R.L. Steiner, and B.F. Fields, Trans. Instrum. meas.36, 258 (1987)
  64. ↑ C. A. Hamilton, and Y. H. Tang, Metrologia, 36, 53 (1999)
  65. ↑ Guide to the Expression of Uncertainty in Measurement, Geneva, International Organization for Standardization (1995)
This article is issued from Wikipedia - version of the 10/5/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.