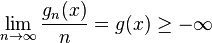Kingman's subadditive ergodic theorem

In mathematics, Kingman's subadditive ergodic theorem is one of several ergodic theorems. It can be seen as a generalization of Birkhoff's ergodic theorem.^[1] Intuitively, the subadditive ergodic theorem is a kind of random variable version of Fekete's lemma (hence the name ergodic).^[2] As a result, it can be rephrased in the language of probability, e.g. using a sequence of random variables and expected values. The theorem is named after John Kingman.

Statement of theorem

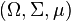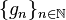Let $T$ be a measure-preserving transformation on the probability space $(\Omega,\Sigma,\mu)$ , and let $\{g_n\}_{n\in\mathbb{N}}$ be a sequence of 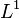$L^1$ functions such that 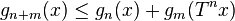$g_{n+m}(x)\le g_n(x)+g_m(T^nx)$ (subadditivity relation). Then

\lim_{n\to\infty}\frac{g_n(x)}{n}=g(x)\ge-\infty

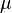for $\mu$ -a.e. x, where g(x) is T-invariant. If T is ergodic, then g(x) is a constant.

Applications

If we take 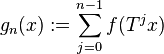$g_n(x):=\sum_{j=0}^{n-1}f(T^jx)$ , then we have additivity and we get Birkhoff's pointwise ergodic theorem.

Kingman's subadditive ergodic theorem can be used to prove statements about Lyapunov exponents. It also has applications to percolations and probability/random variables.^[3]

References

↑ S. Lalley, Kingman's subadditive ergodic theorem lecture notes, http://galton.uchicago.edu/~lalley/Courses/Graz/Kingman.pdf
↑ http://math.nyu.edu/degree/undergrad/Chen.pdf
↑ Pitman, Lecture 12: Subadditive ergodic theory, http://www.stat.berkeley.edu/~pitman/s205s03/lecture12.pdf

External links

Theorem proof (Steele)

This article is issued from Wikipedia - version of the 5/24/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.