Kirsch equations
The Kirsch equations describe the elastic stresses around the hole in an infinite plate in one directional tension. They are named after Ernst Gustav Kirsch.
Result
Loading an infinite plate with circular hole of radius a with stress σ, the resulting stress field is:
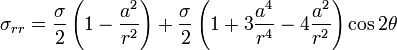
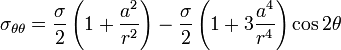
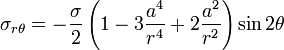
References
- Kirsch, 1898, Die Theorie der Elastizität und die Bedürfnisse der Festigkeitslehre. Zeitschrift des Vereines deutscher Ingenieure, 42, 797–807.
This article is issued from Wikipedia - version of the 11/19/2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.