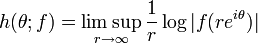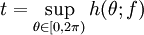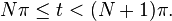Lidstone series

In mathematics, a Lidstone series, named after George James Lidstone, is a kind of polynomial expansion that can expressed certain types of entire functions.

Let ƒ(z) be an entire function of exponential type less than (N + 1)π, as defined below. Then ƒ(z) can be expanded in terms of polynomials A_n as follows:

f(z)=\sum_{n=0}^\infty \left[ A_n(1-z) f^{(2n)}(0) + A_n(z) f^{(2n)}(1) \right] + \sum_{k=1}^N C_k \sin (k\pi z).

Here A_n(z) is a polynomial in z of degree n, C_k a constant, and ƒ⁽ⁿ⁾(a) the nth derivative of ƒ at a.

A function is said to be of exponential type of less than t if the function

h(\theta; f) = \underset{r\to\infty}{\limsup}\, \frac{1}{r} \log |f(r e^{i\theta})|\,

is bounded above by t. Thus, the constant N used in the summation above is given by

t= \sup_{\theta\in [0,2\pi)} h(\theta; f)\,

with

N\pi \leq t < (N+1)\pi.\,

References

Ralph P. Boas, Jr. and C. Creighton Buck, Polynomial Expansions of Analytic Functions, (1964) Academic Press, NY. Library of Congress Catalog 63-23263. Issued as volume 19 of Moderne Funktionentheorie ed. L.V. Ahlfors, series Ergebnisse der Mathematik und ihrer Grenzgebiete, Springer-Verlag ISBN 3-540-03123-5

This article is issued from Wikipedia - version of the 5/5/2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.