Lulu smoothing

In signal processing, Lulu smoothing is a non-linear mathematical technique for removing impulsive noise from a data sequence such as a time series. It is a non-linear equivalent to taking a moving average (or other smoothing technique) of a time series, and is similar to other non-linear smoothing techniques, such as Tukey[1] or median smoothing.

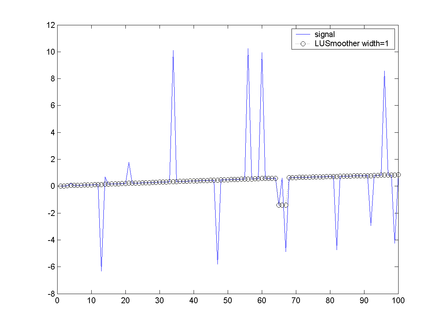
LU smoother of width 1 applied to a noisy sequence

LULU smoothers are compared in detail to median smoothers by Jankowitz[2] and found to be superior in some aspects, particularly in mathematical properties like idempotence.

Properties

Lulu operators have a number of attractive mathematical properties, among them idempotence – meaning that repeated application of the operator yields the same result as a single application – and co-idempotence. An interpretation of idempotence is that: 'Idempotence means that there is no “noise” left in the smoothed data and co-idempotence means that there is no “signal” left in the residual.'[3]

When studying smoothers there are four properties that are useful to optimize:[4]

  1. Effectiveness
  2. Consistency
  3. Stability
  4. Efficiency

The operators can also be used to decompose a signal into various subcomponents[5] similar to wavelet or Fourier decomposition.

History

Lulu smoothers were discovered by C. H. Rohwer[6][7] and have been studied for the last 30 years. Their exact and asymptotic distributions have been derived.[3]

Operation

Applying a Lulu smoother consists of repeated applications of the min and max operators over a given subinterval of the data. As with other smoothers, a width or interval must be specified. The Lulu smoothers are composed of repeated applications of the L (lower) and U (Upper) operators, which are defined as follows:

L operator

For an L operator of width n over an infinite sequence of xs (..., xj, xj+1,...), the operation on xj is calculated as follows:

  1. Firstly we create (n + 1) mini-sequences of length (n + 1) each. Each of these mini-sequences contains the element xj. For example, for width 1, we create 2 mini-sequences of length 2 each. For width 1 these mini sequences are (xj−1, xj) and (xj, xj+1). For width 2, the mini-sequences are (xj−2, xj−1, xj), (xj−1, xj, xj+1) and (xj, xj+1, xj+2). For width 2, we refer to these mini-sequences as seq−1, seq0 and seq+1
  2. Then we take the minimum of each of the mini sequences. Again for width 2 this gives: (Min(seq−1), Min(seq0), Min(seq+1)). This gives us (n + 1) numbers for each point.
  3. Lastly we take the maximum of (the minimums of the mini sequences), or Max(Min(seq−1), Min(seq0), Min(seq+1)) and this becomes L(xj)

Thus for width 2, the L operator is:

L(xj) = Max(Min(seq−1), Min(seq0), Min(seq+1))

U Operator

This is identical to the L operator, except that the order of Min and Max is reversed, i.e. for width 2:

U(xj) = Min(Max(seq−1), Max(seq0), Max(seq+1))

Examples

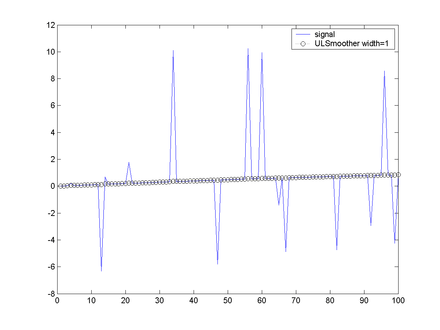
Examples of the U and L operators, as well as combined UL and LU operators on a sample data set are shown in the following figures.

L Smoother width 1
U Smoother width 1

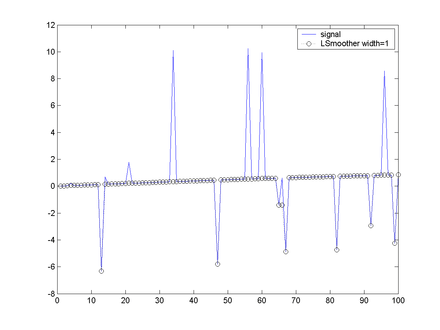
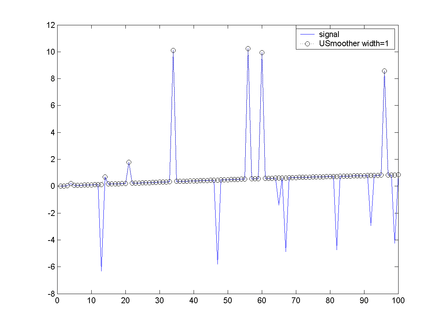
It can be seen that the results of the UL and LU operators can be different. The combined operators are very effective at removing impulsive noise, the only cases where the noise is not removed effectively is where we get multiple noise signals very close together, in which case the filter 'sees' the multiple noises as part of the signal.

LU smoother width 1
UL smoother width 1

References

  1. ↑ Tukey, JW (1974). "Nonlinear (nonsuperposable) methods for smoothing data". Cong. Rec. EASCON: 673.
  2. ↑ Jankowitz, M.D. (2007). "Some statistical aspects of LULU smoothers". PhD. Thesis. Stellenbosch: University of Stellenbosch.
  3. 1 2 Conradie, WJ and de Wet, T. and Jankowitz, M. (2006). "Exact and asymptotic distributions of LULU smoothers". Journal of computational and applied mathematics. Elsevier. 186 (1): 253–267. doi:10.1016/j.cam.2005.03.073.
  4. ↑ Rohwer, Carl (2005). Nonlinear smoothing and multiresolution analysis. 150. Birkhauser Basel.
  5. ↑ Fabris-Rotelli, Inger Nicolette (2009). "LULU operators on multidimensional arrays and applications". MSc. Thesis. University of Pretoria.
  6. ↑ Rohwer, CH (1989). "Idempotent one-sided approximation of median smoothers". Journal of Approximation Theory. Elsevier. 58 (2): 151–163. doi:10.1016/0021-9045(89)90017-8.
  7. ↑ Rohwer, CH (1999). "Projections and separators". Quaestiones Mathematicae. Taylor & Francis. 22 (2): 219–230. doi:10.1080/16073606.1999.9632077.
This article is issued from Wikipedia - version of the 12/3/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.