Mitotic exit

Mitotic Exit is an important transition point that signifies the end of mitosis and the onset of new G1 phase for a cell, and the cell needs to rely on specific control mechanisms to ensure that once it exits mitosis, it never returns to mitosis until it has gone through G1, S, and G2 phases and passed all the necessary checkpoints. Many factors including cyclins, cyclin-dependent kinases (CDKs), ubiquitin ligases, inhibitors of cyclin-dependent kinases, and reversible phosphorylations regulate mitotic exit to ensure that cell cycle events occur in correct order with least amount of errors.[1] The end of mitosis is characterized by spindle breakdown, shortened kinetochore microtubules, and pronounced outgrowth of astral (non-kinetochore) microtubules. For a normal eukaryotic cell, mitotic exit is irreversible.[2]

Proteolytic degradation

Fig. 1 Immunofluorescence patterns of cyclin B and phosphorylated cyclin-dependent kinase1 (Cdk1) in HeLa cells change as they go from G2 to anaphase.

Many speculations were made with regard to the control mechanisms employed by a cell to promote the irreversibility of mitotic exit in a eukaryotic model organism, the budding yeast Saccharomyces cerevisiae. Proteolytic degradation of cell cycle regulators and corresponding effects on the levels of cyclin-dependent kinases were proposed as a mechanism that promotes eukaryotic cell cycle and metaphase-to-anaphase transition in particular. In this theory, anaphase promoting complex (APC), a class of ubiquitin ligase, facilitates degradation of mitotic cyclins (Clb2) and anaphase-inhibiting factors (PDS1, CUT2) to promote mitotic exit.[3] APC ubiquitinates nine-amino acid motif known as the destruction box (D box) in the NH2-terminal domain of mitotic cyclins for degradation by proteasome.[3] APC in association with Cdc20 (APC-Cdc20) ubiquitinates and targets mitotic cyclins (Clb2) for degradation at initial phase. Simultaneously, APC-Cdc20 mediates degradation of securins, which inhibit separases through binding, at anaphase onset. Released and active separase cleaves cohesin that held sister chromatids together, facilitating separation of sister chromatids and initiates mitotic exit by promoting release of Cdc14 from nucleolus.[4][5] At later phase, downregulation of Cdk1 and activation of Cdc14, a Cdh1-activating phosphatase, promotes formation of APC in association with Cdh1 (APC-Cdh1) to degrade Clb2s.[2] Cdc20 and Cdh1, which are the activators of APC, recruit substrates such as securin and B-type cyclins(Clb) for ubiquitination.[6] Without Cdk1-Clb2 complexes to phosphorylate proteins that are involved in spindle dynamics such as Sli15, Ase1, and Ask1, spindle elongation and chromosomal segregation are promoted, facilitating mitotic exit.[2] The importance of proteolytic degradation in eukaryotic cell cycle changed the view of cell division as a simple kinase cascade to a more complex process in which interactions among phosphorylation, ubiquitination, and proteolysis are necessary.[3] However, experiments using budding yeast cells with cdc28-as1, a INM-PP1 (ATP analog)-sensitive Cdk allele, proved that destruction of B-type cyclins (Clb) is not necessary for triggering irreversible mitotic exit.[2] Clb2 degradation did shorten the Cdk1-inhibition period required for triggering irreversible mitotic exit indicating that cyclin proteolysis contributes to the dynamic nature of the eukaryotic cell cycle due to slower timescale of its action but is unlikely to be the major determining factor in triggering irreversible cell cycle transitions.[2]

Sic1 levels

Discoveries were made which indicated the importance of the level of the inhibitors of cyclin-dependent kinases in regulating eukaryotic cell cycle. In particular, the level of Sic1, a stoichiometric inhibitor of Clb-CDK complexes in budding yeast, was shown to be particularly important in irreversible G1-S transition by irreversibly activating S phase kinases.[7] Sic1 level was shown to play a major role in triggering irreversible mitotic exit (M-G1 transition) as well as in G1-S transition. During mitosis, decreasing levels of Cdk1 leads to the activation of Cdc14, a phosphatase that counteracts Cdk1 via activation of Cdh1 and Swi5, a transcriptional activator of Sic1 proteins.[8] While degradation of Sic1 to a certain low level triggered the onset of S phase, accumulation of Sic1 to a certain high level was required to trigger irreversible mitotic exit.[2] Cdk1-inhibitors could induce mitotic exit even when degradation of B-type cyclins was blocked by expression of non-degradable Clbs or proteasome inhibitors. However, sister chromatids failed to segregate, and cells reverted to mitosis once the inhibitors were washed away, indicating that a threshold level of the inhibitors needs to be achieved to trigger irreversible mitotic exit independently of cyclin degradations.[9] Despite different thresholds of Sic1 level that are required to trigger mitotic exit compared to G1-S transition, the level of Sic1 was shown to play a key role in regulating eukaryotic cell cycle by inhibiting the activity of CDKs.

Dynamical systems approach

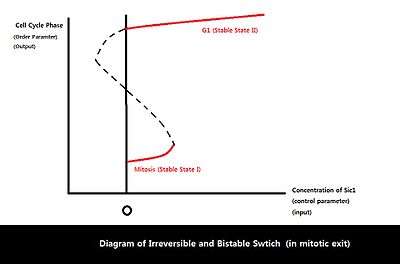
Fig. 1 Irreversible and bistable switch in mitotic exit with control parameter being Sic1 level and order parameter being cell cycle phases.

Because eukaryotic cell cycle involves a variety of proteins and regulatory interactions, dynamical systems approach can be taken to simplify a complex biological circuit into a general framework for better analysis.[10][11] Among the four possible input/output relationships, the relationship between Sic1 level and mitotic exit seems to show the characteristics of an irreversible bistable switch, driven by feedback between APC-Cdh1, Sic1, and Clb2-Cdk1.[2] Bistability is known to control biological functions such as cell cycle control and cellular differentiation and play a key role in many cellular regulatory networks.[12] Bistable input/output relationship is characterized by two stable states with two bifurcation points. Multiple outputs are possible for one specific input in the region of bistability, marked by two bifurcation points. In addition, the bistable relationship displays hysteresis: the final state/output depends on the history of the input as well as the current value of input because the system has a memory.[10] One bifurcation point has a negative control parameter value (the bifurcation point is on the other side of the axis), resulting in disconnection between the two stable states and irreversibility of the transition from one state to the other. With regard to mitotic exit, the two stable states are defined by mitosis and G1 phase. Once Sic1 level (input) accumulates beyond the threshold, irreversible transition occurs from mitosis (stable state I) to G1 phase (stable state II). In the imperfect environment, the only bifurcation that remains intact is saddle-node bifurcation. Saddle-node bifurcation does not break down (saddle-node is the expected generic behavior), while transcritical and pitchfork bifurcations break down in the presence of imperfections.[13] Thus, the only one-dimensional bifurcation that can exist in imperfect biological world is the saddle-node bifurcation.[10] The bistable relation between M-G1 transition and Sic1 level can be represented as a diagram of two saddle-node bifurcations in which the system’s behavior changes qualitatively with a small change in control parameter, the amount of Sic1.

Systems-level feedback

Fig. 2 Simplified network involving Cdk1-Clb2, APC-Cdh1, Sic1, and Cdc14. Double negative feedback loop, mediated by APC-Cdh1 and Sic1, is required to suppress Cdk1-Clb2 and trigger mitotic exit.

Because the behavior of cell cycle critically depends on the amount of Sic1 at the M-G1 transition state, the amount of Sic1 is tightly regulated by systems-level feedbacks. Because Cdk1-Clb2 inhibits Sic1 by phosphorylating Sic1 and making Sic1 available for degradation via ubiquitylation, APC-Cdh1-dependent degradation of Cdk1-Clb2 not only decreases the level of available Cdk1-Clb2 complexes but also increases the level of Sic1 which in turn further inhibits the function of Cdk1-Clb2.[8] This activation of the double negative feedback loop is initiated from APC-Cdc20-dependent degradation of Cdk1-Clb2 and release of Cdc14 from nucleolar protein Net1/Cfi1.[14] FEAR (Cdc14 early anaphase release) pathway facilitates Clb2-Cdk1-dependent phosphorylation of Net1 which transiently releases Cdc14 from Net1.[15] The released Cdc14 and Clb2-Cdk1 complexes go onto form spindles that activates mitotic exit network (MEN). MEN allows sustained release of Cdc14 from the nucleolus,[15] and Cdc14 counters the activity of Clb2-Cdk1 by activating Cdh1 and stabilizing Sic1 through activation of Sic1-transcriptional activator Swi5.[16] Sic1 positively regulates itself by inhibiting Cdk1-Clb2 to release inhibition of Swi5, and Cdh1 also positively regulates itself by inhibiting Clb2-Cdk1 to release inhibition of MEN which can activate Cdc14 and subsequently Cdh1 itself. The double-negative feedback loop, formed by APC-Cdh1 and Sic1, is required to maintain low Clb2-Cdk1 activity because Clb2 auto-activates its synthesis by activating transcriptional factors, Fkh2–Mcm1 Ndd1 complex.[8]

Implications

Eukaryotic cell cycle consists of various checkpoints and feedback loops to ensure faithful and successful cell division. During mitosis for example, when duplicated chromosomes are improperly attached to mitotic spindle, spindle assembly checkpoint (SAC) proteins including Mad and Bub inhibit APC-Cdc20 to delay entry into anaphase and B-type cyclin degradations. In addition, when mitotic spindles are misaligned, MEN and subsequently Cdc14 are inhibited in a Bub2 and Bfa1-dependent manner to prevent degradation of mitotic cyclins and anaphase entry.[16] Sic1 is a nice example demonstrating how systems-level feedbacks interact to sense the environmental conditions and trigger cell cycle transitions. Even though actual M-G1 transition is vastly complex with numerous proteins and regulations involved, dynamical systems approach allows simplification of this complex system into bistable input/output relation with two saddle-node bifurcations in which the output (mitotic exit) depends on critical concentration of Sic1. Using one-dimensional analysis, it might be possible to explain many of the irreversible transition points in the eukaryotic cell cycle that are governed by systems-level control and feedback. Other examples of irreversible transition points include Start (irreversible commitment to a new cell division cycle) that can be explained by irreversible bistable switch whose control parameter is tightly regulated by the systemic feedbacks involving Cln2, Whi5, and SBF.[17]

References

  1. ↑ Erich A. Nigg (2005). "Cyclin-dependent protein kinases: key regulators of the eukaryotic cell cycle". BioEssays. 17 (6): 471–480. doi:10.1002/bies.950170603. PMID 7575488.
  2. 1 2 3 4 5 6 7 Sandra Lo´pez-Avile´s, Orsolya Kapuy, Be´la Nova´k, Frank Uhlmann (2009). "Irreversibility of mitotic exit is the consequence of systems-level feedback". Nature Letters. 459: 592–595. doi:10.1038/nature07984.
  3. 1 2 3 Randall W. King; Raymond J. Deshaies; Jan-Michael Peters; Marc W. Kirschner (1996). "How proteolysis drives the cell cycle". Science. 274 (5293): 1652–1659. doi:10.1126/science.274.5293.1652. PMID 8939846.
  4. ↑ I. Waizenegger; JF. Giménez-Abián; D. Wernic; JM. Peters (2002). "Regulation of Human Separase by Securin Binding and Autocleavage". Current Biology. 12: 1368–1378. doi:10.1016/S0960-9822(02)01073-4. PMID 12194817.
  5. ↑ Matt Sullivan, Frank Uhlmann (2003). "A non-proteolytic function of separase links anaphase onset to mitotic exit". Nat Cell Biol. 5: 249–254. doi:10.1038/ncb940.
  6. ↑ Rosella Visintin; Susanne Prinz; Angelika Amon (1997). "CDC20 and CDH1: A Family of Substrate-Specific Activators of APC-Dependent Proteolysis". Science. 278 (5337): 460–463. doi:10.1126/science.278.5337.460. PMID 9334304.
  7. ↑ Steven I. Reed (2003). "Ratchets and clocks: the cell cycle, ubiquitylation and protein turnover". Nature Reviews Molecular Cell Biology. 4: 855–864. doi:10.1038/nrm1246.
  8. 1 2 3 P. K. Vinod, Paula Freire, Ahmed Rattani, Andrea Ciliberto, Frank Uhlmann, and Bela Novak (2011). "Computational modeling of mitotic exit in budding yeast: the role of separase and Cdc14 endocycles". J.R.Soc.Interface. 8: 1128–1141. doi:10.1098/rsif.2010.0649.
  9. ↑ Tamara A. Potapova; John R. Daum; Bradley D. Pittman; Joanna R. Hudson; Tara N. Jones; David L. Satinover; P. Todd Stukenberg & Gary J. Gorbsky (2006). "The reversibility of mitotic exit in vertebrate cells". Nature Letters. 440: 954–958. doi:10.1038/nature04652.
  10. 1 2 3 Strogatz, Steven H, ed. (1994). "Chapter 2 and 3". Nonlinear dynamics and chaos : with applications to physics, biology, chemistry, and engineering. Perseus Books.
  11. ↑ John J. Tyson, Attila Csikasz-Nagy, and Bela Novak (2002). "The dynamics of cell cycle regulation". BioEssays. 24 (12): 1095–1109. doi:10.1002/bies.10191.
  12. ↑ Dan Siegal-Gaskins; Maria Katherine Mejia-Guerra; Gregory D. Smith; Erich Grotewold (2011). "Emergence of Switch-Like Behavior in a Large Family of Simple Biochemical Networks". PLOS Computational Biology. 7 (5): 1–12. doi:10.1371/journal.pcbi.1002039.
  13. ↑ Crawford, John (1991). "Introduction to Bifurcation Theory". Reviews of Modern Physics. 63: 991–1037. doi:10.1103/revmodphys.63.991.
  14. ↑ Visintin R, Hwang ES, Amon A (1999). "Cfi1 prevents premature exit from mitosis by anchoring Cdc14 phosphatase in the nucleolus". Nature. 398: 818–823. doi:10.1038/19775.
  15. 1 2 A. Lindqvist; W. van Zon; Rosenthal C. Karlsson; RM. Wolthuis (2007). "Cyclin B1–Cdk1 Activation Continues after Centrosome Separation to Control Mitotic Progression". PLOS Biology. 5 (5): 1127–1137. doi:10.1371/journal.pbio.0050123.
  16. 1 2 Joanna Bloom; Frederick R. Cross (2007). "Multiple levels of cyclin specificity in cell-cycle control". Nature Reviews Molecular Cell Biology. 8: 149–160. doi:10.1038/nrm2105. PMID 17245415.
  17. ↑ Charvin G, Oikonomou C, Siggia ED, Cross FR (2010). "Origin of Irreversibility of Cell Cycle Start in Budding Yeast". PLOS Biology. 8 (1): 1–13.
This article is issued from Wikipedia - version of the 10/10/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.