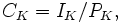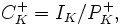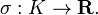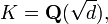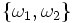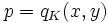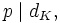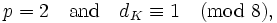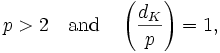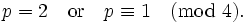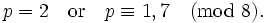Narrow class group
In algebraic number theory, the narrow class group of a number field K is a refinement of the class group of K that takes into account some information about embeddings of K into the field of real numbers.
Formal definition
Suppose that K is a finite extension of Q. Recall that the ordinary class group of K is defined to be
where IK is the group of fractional ideals of K, and PK is the group of principal fractional ideals of K, that is, ideals of the form aOK where a is a unit of K.
The narrow class group is defined to be the quotient
where now PK+ is the group of totally positive principal fractional ideals of K; that is, ideals of the form aOK where a is a unit of K such that σ(a) is positive for every embedding
Uses
The narrow class group features prominently in the theory of representing of integers by quadratic forms. An example is the following result (Fröhlich and Taylor, Chapter V, Theorem 1.25).
- Theorem. Suppose that
- where d is a square-free integer, and that the narrow class group of K is trivial. Suppose that
- is a basis for the ring of integers of K. Define a quadratic form
-
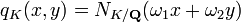 ,
,
-
- where NK/Q is the norm. Then a prime number p is of the form
-
- for some integers x and y if and only if either
-
- or
-
- or
- where dK is the discriminant of K, and
- indicates the Legendre symbol.
Examples
For example, one can prove that the quadratic fields Q(√−1), Q(√2), Q(√−3) all have trivial narrow class group. Then, by choosing appropriate bases for the integers of each of these fields, the above theorem implies the following:
- A prime p is of the form p = x2 + y2 for integers x and y if and only if
- (This is known as Fermat's theorem on sums of two squares.)
- A prime p is of the form p = x2 − 2y2 for integers x and y if and only if
- A prime p is of the form p = x2 − xy + y2 for integers x and y if and only if
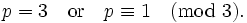 (cf. Eisenstein prime)
(cf. Eisenstein prime)
See also
References
- A. Fröhlich and M. J. Taylor, Algebraic Number Theory (p. 180), Cambridge University Press, 1991.