Non-abelian group

Algebraic structure → Group theory Group theory
Basic notions Subgroup Normal subgroup Quotient group (Semi-)direct product Group homomorphisms kernel image direct sum wreath product simple finite infinite continuous multiplicative additive cyclic abelian dihedral nilpotent solvable List of group theory topics
Finite groups Classification of finite simple groups cyclic alternating Lie type sporadic Lagrange's theorem Sylow theorems Hall's theorem p-group Elementary abelian group Frobenius group Schur multiplier Symmetric group Sn Klein four-group V Dihedral group Dn Quaternion group Q Dicyclic group Dicn
Discrete groups Lattices Integers (Z) Lattice Modular groups PSL(2,Z) SL(2,Z)
Topological / Lie groups Solenoid Circle General linear GL(n) Special linear SL(n) Orthogonal O(n) Euclidean E(n) Special orthogonal SO(n) Unitary U(n) Special unitary SU(n) Symplectic Sp(n) G2 F4 E6 E7 E8 Lorentz Poincaré Conformal Diffeomorphism Loop Infinite dimensional Lie group O(∞) SU(∞) Sp(∞)
Algebraic groups Elliptic curve Linear algebraic group Abelian variety

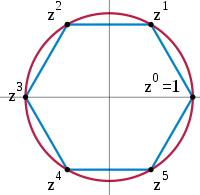
In mathematics, and specifically in group theory, a nonabelian group, sometimes called a noncommutative group, is a group ( G, ∗ ) in which there exists at least one pair of elements a and b of G, such that a ∗ b ≠ b ∗ a.^[1][2] This class of groups contrasts with the abelian groups. (In an abelian group, all pairs of group elements commute).

Nonabelian groups are pervasive in mathematics and physics. One of the simplest examples of a nonabelian group is the dihedral group of order 6. It is the smallest finite nonabelian group. A common example from physics is the rotation group SO(3) in three dimensions (rotating something 90 degrees away from you and then 90 degrees to the left is not the same as doing them the other way round).

Both discrete groups and continuous groups may be nonabelian. Most of the interesting Lie groups are nonabelian, and these play an important role in gauge theory.

See also

• Associative algebra
• Noncommutative geometry
• Niels Henrik Abel

References