Stacking (chemistry)

Three representative conformations of the benzene dimer

In chemistry, pi stacking (also called π–π stacking) refers to attractive, noncovalent interactions between aromatic rings, since they contain pi bonds. These interactions are important in nucleobase stacking within DNA and RNA molecules, protein folding, template-directed synthesis, materials science, and molecular recognition, although new research suggests that pi stacking may not be operative in some of these applications. Despite intense experimental and theoretical interest, there is no unified description of the factors that contribute to pi stacking interactions.

Evidence for pi stacking

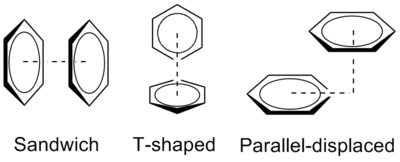
The benzene dimer is the prototypical system for the study of pi stacking, and is experimentally bound by 8–12 kJ/mol (2–3 kcal/mol) in the gas phase with a separation of 4.96 Å between the centers of mass for the T-shaped dimer. The small binding energy makes the benzene dimer difficult to study experimentally, and the dimer itself is only stable at low temperatures and is prone to cluster.[1]

Other evidence for pi stacking comes from X-ray crystal structures. Perpendicular and offset parallel configurations can be observed in the crystal structures of many simple aromatic compounds.[1] Similar offset parallel or perpendicular geometries were observed in a survey of high-resolution x-ray protein crystal structures in the Protein Data Bank. Analysis of the aromatic amino acids phenylalanine, tyrosine, histidine, and tryptophan indicates that dimers of these side chains have many possible stabilizing interactions at distances larger than the average van der Waals radii.[2]

Geometric configurations

The preferred geometries of the benzene dimer have been modeled at a high level of theory with MP2-R12/A computations and very large counterpoise-corrected aug-cc-PVTZ basis sets.[1] The two most stable conformations are the parallel displaced and T-shaped, which are essentially isoenergetic and represent energy minima. In contrast, the sandwich configuration maximizes overlap of the pi system, is least stable, and represents an energetic saddle point. This later finding is consistent with a relative rarity of this configuration in x-ray crystal data.

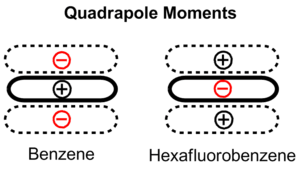
The relative binding energies of these three geometric configurations of the benzene dimer can be explained by a balance of quadrupole/quadrupole and London dispersion forces. While benzene does not have a dipole moment, it has a strong quadrupole moment.[3] The local C-H dipole means that there is positive charge on the atoms in the ring and a correspondingly negative charge representing an electron cloud above and below the ring. The quadrupole moment is reversed for hexafluorobenzene due to the electronegativity of fluorine. The benzene dimer in the sandwich configuration is stabilized by London dispersion forces but destabilized by repulsive quadrupole/quadrupole interactions. By offsetting one of the benzene rings, the parallel displaced configuration reduces these repulsive interactions and is stabilized. The T-shaped configuration enjoys favorable quadrupole/quadrupole interactions, as the positive quadrupole of one benzene ring interacts with the negative quadrupole of the other. The benzene rings are furthest apart in this configuration, so the favorable quadrupole/quadrupole interactions evidently compensate for diminished dispersion forces.

Quadrupole moments of benzene and hexafluorobenzene. The polarity is inverted due to differences in electronegativity for hydrogen and fluorine relative to carbon.

Substituent effects

The ability to fine-tune pi stacking interactions would be useful in numerous synthetic efforts. One example would be to increase the binding affinity of a small-molecule inhibitor to an enzyme pocket containing aromatic residues. The effects of substituents on pi stacking interactions is difficult to model and a matter of debate.

Electrostatic model

An early model for the role of substituents in pi stacking interactions was proposed by Hunter and Sanders.[4] They used a simple mathematical model based on sigma and pi atomic charges, relative orientations, and van der Waals interactions to qualitatively determine that electrostatics are dominant in substituent effects. According to their model, electron-withdrawing groups reduce the negative quadropole of the aromatic ring and thereby favor parallel displaced and sandwich conformations. Contrastingly, electron donating groups increase the negative quadropole, which may increase the interaction strength in a T-shaped configuration with the proper geometry. Based on this model, the authors proposed a set of rules governing pi stacking interactions which prevailed until more sophisticated computations were applied.

Experimental evidence for the Hunter-Sanders model was provided by Siegel et al. using a series of substituted syn- and anti-1,8-di-o-tolylnaphthalenes.[5] In these compounds the aryl groups "face-off" in a stacked geometry due to steric crowding, and the barrier to epimerization was measured by nuclear magnetic resonance spectroscopy. The authors reported that aryl rings with electron-withdrawing substituents had higher barriers to rotation. The interpretation of this result was that these groups reduced the electron density of the aromatic rings, allowing more favorable sandwich pi stacking interactions and thus a higher barrier. In other words, the electron-withdrawing groups resulted in "less unfavorable" electrostatic interactions in the ground state.

Hunter et al. applied a more sophisticated chemical double mutant cycle with a hydrogen-bonded "zipper" to the issue of substituent effects in pi stacking interactions.[6] This technique has been used to study a multitude of noncovalent interactions. The single mutation, in this case changing a substituent on an aromatic ring, results in secondary effects such as a change in hydrogen bond strength. The double mutation quantifies these secondary interactions, such that even a weak interaction of interest can be dissected from the array. Their results indicate that more electron-withdrawing substituents have less repulsive pi stacking interactions. Correspondingly, this trend was exactly inverted for interactions with pentafluorophenylbenzene, which has a quadruple moment equal in magnitude but opposite in sign as that of benzene.[3] The findings provide direct evidence for the Hunter-Sanders model. However, the stacking interactions measured using the double mutant method were surprisingly small, and the authors note that the values may not be transferrable to other systems.

In a follow-up study, Hunter et al. verified to a first approximation that the interaction energies of the interacting aromatic rings in a double mutant cycle are dominated by electrostatic effects.[7] However, the authors note that direct interactions with the ring substituents, discussed below, also make important contributions. Indeed, the interplay of these two factors may result in the complicated substituent- and geometry-dependent behavior of pi stacking interactions.

Double mutant cycle used by Hunter et al.[6] to probe T-shaped π-stacking interactions

Direct Interaction model

The Hunter-Sanders model has been criticized by numerous research groups offering contradictory experimental and computational evidence of pi stacking interactions that are not governed primarily by electrostatic effects.

The clearest experimental evidence against electrostatic substituent effects was reported by Rashkin and Waters.[8] They used meta- and para-substituted N-benzyl-2-(2-fluorophenyl)-pyridinium bromides, which stack in a parallel displaced conformation, as a model system for pi stacking interactions. In their system, a methylene linker prohibits favorable T-shaped interactions. As in previous models, the relative strength of pi stacking interactions was measured by NMR as the rate of rotation about the biaryl bond, as pi stacking interactions are disrupted in the transition state. Para-substituted rings had small rotational barriers which increased with increasingly electron-withdrawing groups, consistent with prior findings. However, meta-substituted rings had much larger barriers of rotation despite having nearly identical electron densities in the aromatic ring. The authors explain this discrepancy as direct interaction of the edge of hydrogen atoms of one ring with the electronegative substituents on the other ring. This claim is supported by chemical shift data of the proton in question.

Much of the detailed analyses of the relative contributions of factors in pi stacking have been borne out by computation. Sherill and Sinnokrot reported a surprising finding using high-level theory that all substituted benzene dimers have more favorable binding interactions than a benzene dimer in the sandwich configuration.[9] Later computational work from the Sherill group revealed that the substituent effects for the sandwich configuration are additive, which points to a strong influence of dispersion forces and direct interactions between substituents.[10] It was noted that interactions between substituted benzenes in the T-shaped configuration were more complex. Finally, Sherril and Sinnokrot argue in their review article that any semblance of a trend based on electron donating or withdrawing substituents can be explained by exchange-repulsion and dispersion terms.[11]

Houk and Wheeler also provide compelling computational evidence for the importance of direct interaction in pi stacking.[12] In their analysis of substituted benzene dimers in a sandwich conformation, they were able to recapitulate their findings using an exceedingly simple model where the substituted benzene, Ph-X, was replaced by H-X. Remarkably, this crude model resulted in the same trend in relative interaction energies, and correlated strongly with the values calculated for Ph-X. This finding suggests that substituent effects in the benzene dimer are due to direct interaction of the substituent with the aromatic ring, and that the pi system of the substituted benzene is not involved. This latter point is expanded upon below.

Houk and Wheeler's [12] computational model of substituent direct interactions in pi stacking.

In summary, it would seem that the relative contributions of electrostatics, dispersion, and direct interactions to the substituent effects seen in pi stacking interactions are highly dependent on geometry and experimental design. The lack of consensus on the matter may simply reflect the complexity of the issue.

Requirement for aromaticity

The conventional understanding of pi stacking involves quadropole interactions between delocalized electrons in p-orbitals. In other words, aromaticity should be required for this interaction to occur. However, several groups have provided contrary evidence, calling into question whether pi stacking is a unique phenomenon or whether it extends to other neutral, closed-shell molecules.

In an experiment not dissimilar from others mentioned above, Paliwal et al. constructed a molecular torsion balance from an aryl ester with two conformational states.[13] The folded state had a well-defined pi stacking interaction with a T-shaped geometry, whereas the unfolded state had no aryl-aryl interactions. The NMR chemical shifts of the two conformations were distinct and could be used to determine the ratio of the two states, which was interpreted as a measure of intramolecular forces. Interestingly, the authors report that a preference for the folded state is not unique to aryl esters. For example, the cyclohexyl ester favored the folded state more so than the phenyl ester, and the tert-butyl ester favored the folded state by a preference greater than that shown by any aryl ester. This suggests that aromaticity is not a strict requirement for favorable interaction with an aromatic ring.

Other evidence for non-aromatic pi stacking interactions results from computation analysis. Grimme reported that the interaction energies of smaller dimers consisting of one or two rings are very similar for both aromatic and saturated compounds.[14] This finding is of particular relevance to biology, and suggests that the contribution of pi systems to phenomena such as stacked nucleobases may be overestimated. However, it was shown that an increased stabilizing interaction is seen for large aromatic dimers. As previously noted, this interaction energy is highly dependent on geometry. Indeed, large aromatic dimers are only stabilized relative to their saturated counterparts in a sandwich geometry, while their energies are similar in a T-shaped interaction.

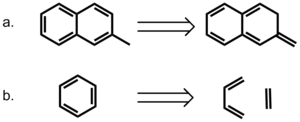
A more direct approach to modeling the role of aromaticity was taken by Bloom and Wheeler.[15] The authors compared the interactions between benzene and either 2-methylnaphthalene or its non-aromatic isomer, 2-methylene-2,3-dihydronaphthalene. The later compound provides a means of conserving the number of p electrons but removing the effects of delocalization. Surprisingly, the interaction energies with benzene are higher for the non-aromatic compound, suggesting that pi-bond localization is favorable in pi stacking interactions. The authors also considered a homodesmotic dissection of benzene into ethylene and 1,3-butadiene and compared these interactions in a sandwich with benzene. Their calculation indicates that the interaction energy between benzene and homodesmotic benzene is higher than that of a benzene dimer in both sandwich and parallel displaced conformations, again highlighting the favorability of localized pi-bond interactions. These results strongly suggest that aromaticity is not required for pi stacking interactions in this model.

a) Substituted naphthalenes and b) Homodesmotic dissection of benzene used by Bloom and Wheeler[15] to quantify the effects of delocalization on pi stacking.

Even in light of this evidence, Grimme concludes that pi stacking does indeed exist.[14] However, he cautions that smaller rings, particularly those in T-shaped conformations, do not behave significantly differently from their saturated counterparts, and that the term should be specified for larger rings in stacked conformations which do seem to exhibit a cooperative pi electron effect.

Applications of pi stacking

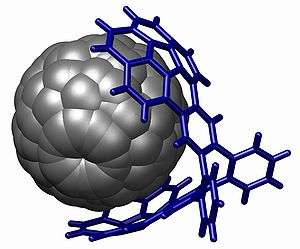
A powerful demonstration of stacking is found in the buckycatcher.[16] This molecular tweezer is based on two concave buckybowls with a perfect fit for one convex fullerene molecule. Complexation takes place simply by evaporating a toluene solution containing both compounds. In solution an association constant of 8600 M−1 is measured based on changes in NMR chemical shifts.

Crystal structure of a fullerene bound in a buckycatcher through aromatic stacking interactions. Reported by Sygula and coworkers.[16]

Pi stacking is prevalent in protein crystal structures, and also contributes to the interactions between small-molecules and proteins. As a result, pi-pi and cation-pi interactions are important factors in rational drug design.[17] One example is the FDA-approved acetylcholinesterase (AChE) inhibitor tacrine which is used in the treatment of Alzheimer's disease. Tacrine is proposed to have a pi stacking interaction with the indolic ring of Trp84, and this interaction has been exploited in the rational design of novel AChE inhibitors.[18]

Crystal structure of Tacrine bound to acetylcholinesterase (PDB accession: 1ACJ) visualized using UCSF Chimera. A pi stacking interaction between Tacrine (blue) and Trp84 (red) is proposed.

Addition in pharmacological active compounds

Several variants of pi coordinated phenyls have even been tested using transition metals for stacking η6-phenyltropanes, using however, cyclopentadienyl & tricarbonyl in place of a benzene. Which in the case of the tricarbonyl doubled the compound's affinity for its intended ligand site (posited as due to resultant electrostatic influences being more conducive to the target)[19]

See also

External links

References

  1. 1 2 3 Sinnokrot, MO; Valeev, EF; Sherrill, CD (2002). "Estimates of the ab initio limit for pi-pi interactions: The benzene dimer". J. Am. Chem. Soc. 124 (36): 10887–10893. doi:10.1021/ja025896h. PMID 12207544.
  2. ↑ McGaughey, GB; Gagné, M; Rappé, AK (1998). "Pi-Stacking interactions. Alive and well in proteins". J. Biol. Chem. 273 (25): 15458–15463. doi:10.1074/jbc.273.25.15458. PMID 9624131.
  3. 1 2 "The electric quadrupole moments of benzene and hexafluorobenzene". Chem. Phys. Lett. 78 (3): 421–423. 1981. doi:10.1016/0009-2614(81)85228-1.
  4. ↑ Hunter, Christopher A.; Sanders, Jeremy K. M. (1990). "The nature of .pi.-.pi. Interactions". J. Am. Chem. Soc. 112 (14): 5525–5534. doi:10.1021/ja00170a016.
  5. ↑ Cozzi, Franco; Cinquini, Mauro; Annuziata, Rita; Siegel, Jay S. (1993). "Dominance of polar/.pi. Over charge-transfer effects in stacked phenyl interactions". J. Am. Chem. Soc. 115 (12): 5330–5331. doi:10.1021/ja00065a069.
  6. 1 2 Cockroft, SL; Hunter, CA; Lawson, KR; Perkins, J; Urch, CJ (2005). "Electrostatic control of aromatic stacking interactions". J. Am. Chem. Soc. 127 (24): 8594–8595. doi:10.1021/ja050880n. PMID 15954755.
  7. ↑ Cockroft, SL; Perkins, J; Zonta, C; Adams, H; Spey, SE; Low, CM; Vinter, JG; Lawson, KR; Urch, CJ (2007). "Substituent effects on aromatic stacking interactions". Org. Biomol. Chem. 5 (7): 1062–1080. doi:10.1039/b617576g. PMID 17377660.
  8. ↑ Rashkin, MJ; Waters, ML (2002). "Unexpected substituent effects in offset pi-pi stacked interactions in water". J. Am. Chem. Soc. 124 (9): 1860–1861. doi:10.1021/ja016508z. PMID 11866592.
  9. ↑ Sinnokrot, Mutasem Omar; Sherrill, C. David (2003). "Unexpected Substituent Effects in Face-to-Face π-Stacking Interactions". J. Phys. Chem. A. 107 (41): 8377–8379. doi:10.1021/jp030880e.
  10. ↑ Ringer, AL; Sinnokrot, MO; Lively, RP; Sherrill, CD (2006). "The effect of multiple substituents on sandwich and T-shaped pi-pi interactions". Chem. Eur. J. 12 (14): 3821–8. doi:10.1002/chem.200501316. PMID 16514687.
  11. ↑ Sinnokrot, MO; Sherrill, CD (2006). "High-accuracy quantum mechanical studies of pi-pi interactions in benzene dimers". J. Phys. Chem. A. 110 (37): 10656–10668. doi:10.1021/jp0610416. PMID 16970354.
  12. 1 2 Wheeler, SE; Houk, KN (2008). "Substituent effects in the benzene dimer are due to direct interactions of the substituents with the unsubstituted benzene". J. Am. Chem. Soc. 130 (33): 10854–10855. doi:10.1021/ja802849j. PMC 2655233Freely accessible. PMID 18652453.
  13. ↑ Paliwal, S.; Geib, S.; Wilcox, C. S. (1994). "Molecular Torsion Balance for Weak Molecular Recognition Forces. Effects of "Tilted-T" Edge-to-Face Aromatic Interactions on Conformational Selection and Solid-State Structure". J. Am. Chem. Soc. 116 (10): 4497–4498. doi:10.1021/ja00089a057.
  14. 1 2 Angew. Chem. Int. Ed. 200 8, 47, 3430–3434
  15. 1 2 Bloom, Jacob W. G.; Wheeler, Steven E. (2011). "Taking the Aromaticity out of Aromatic Interactions". Angew. Chem. 123 (34): 7993–7995. doi:10.1002/ange.201102982.
  16. 1 2 A. Sygula, F. R. Fronczek, R. Sygula, P. W. Rabideau and M. M. Olmstead (2007). "A Double Concave Hydrocarbon Buckycatcher". J. Am. Chem. Soc. 129 (13): 3842–3843. doi:10.1021/ja070616p. PMID 17348661.
  17. ↑ Babine, RE; Bender, SL (1997). "Molecular Recognition of Proteinminus signLigand Complexes: Applications to Drug Design". Chem. Rev. 97 (5): 1359–1472. doi:10.1021/cr960370z. PMID 11851455.
  18. ↑ J. Mol. Graphics Modell. 25: 169–175. 2005. Missing or empty |title= (help)
  19. ↑ Singh, Satendra; et al. (2000). "Chemistry, Design, and Structure-Activity Relationship of Cocaine Antagonists" (PDF). Chem. Rev. 100: 925–1024.
This article is issued from Wikipedia - version of the 5/25/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.