Pure shear
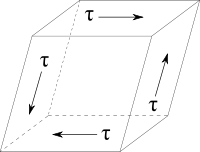
An element in pure shear
In mechanics and geology, pure shear is a three-dimensional homogeneous flattening of a body.[1] It is an example of irrotational strain in which a body is elongated in one direction while being shortened perpendicularly.[2] For soft materials, such as rubber, a strain state of pure shear is often used for characterizing hyperelastic and fracture mechanical behavior. [3] [4] A rod under torsion is a practical example for a body under pure shear.
Pure shear stress-strain relation
Pure shear stress, denoted , is related to pure shear strain, denoted , by the following equation:[5]
where is the shear modulus of the material, given by
Here is Young's modulus and is Poisson's ratio. Combining gives
See also
References
- ↑ Reish, Nathaniel E.; Gary H. Girty. "Definition and Mathematics of Pure Shear". San Diego State University Department of Geological Sciences. Retrieved 24 December 2011.
- ↑ "Pure shear". Answers.com. Retrieved 24 December 2011.
- ↑ "Where do the Pure and Shear come from in the Pure Shear test?" (PDF). Retrieved 12 April 2013.
- ↑ "Comparing Simple Shear and Pure Shear" (PDF). Retrieved 12 April 2013.
- ↑ "Strength of Materials". Eformulae.com. Retrieved 24 December 2011.
This article is issued from Wikipedia - version of the 11/29/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.