Quantitative feedback theory

In control theory, quantitative feedback theory (QFT), developed by Isaac Horowitz (Horowitz, 1963; Horowitz and Sidi, 1972), is a frequency domain technique utilising the Nichols chart (NC) in order to achieve a desired robust design over a specified region of plant uncertainty. Desired time-domain responses are translated into frequency domain tolerances, which lead to bounds (or constraints) on the loop transmission function. The design process is highly transparent, allowing a designer to see what trade-offs are necessary to achieve a desired performance level.

Plant templates

QFT Feedback System

Usually any system can be represented by its Transfer Function (Laplace in continuous time domain), after getting the model of a system.

As a result of experimental measurement, values of coefficients in the Transform Function have a range of uncertainty. Therefore, in QFT every parameter of this function is included into an interval of possible values, and the system may be represented by a family of plants rather than by a standalone expression.

$\mathcal{P}(s) = \left \lbrace \dfrac{\prod_{i} (s + z_i)}{\prod_{j} (s + p_j)}, \forall z_i \in [z_{i,min}, z_{i,max}], p_j \in [p_{j,min}, p_{j,max}] \right \rbrace$

A frequency analysis is performed for a finite number of representative frequencies and a set of templates are obtained in the NC diagram which encloses the behaviour of the open loop system at each frequency.

Frequency bounds

Usually system performance is described as robustness to instability (phase and gain margins), rejection to input and output noise disturbances and reference tracking. In the QFT design methodology these requirements on the system are represented as frequency constraints, conditions that the compensated system loop (controller and plant) could not break.

With these considerations and the selection of the same set of frequencies used for the templates, the frequency constraints for the behaviour of the system loop are computed and represented on the Nichols Chart (NC) as curves.

To achieve the problem requirements, a set of rules on the Open Loop Transfer Function, for the nominal plant 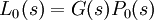$L_0(s) = G(s)P_0(s)$ may be found. That means the nominal loop is not allowed to have its frequency value below the constraint for the same frequency, and at high frequencies the loop should not cross the Ultra High Frequency Boundary (UHFB), which has an oval shape in the center of the NC.

Loop shaping

The controller design is undertaken on the NC considering the frequency constraints and the nominal loop 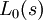$L_0(s)$ of the system. At this point, the designer begins to introduce controller functions ( 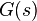$G(s)$ ) and tune their parameters, a process called Loop Shaping, until the best possible controller is reached without violation of the frequency constraints.

The experience of the designer is an important factor in finding a satisfactory controller that not only complies with the frequency restrictions but with the possible realization, complexity, and quality.

For this stage there currently exist different CAD (Computer Aided Design) packages to make the controller tuning easier.

Prefilter design

Finally, the QFT design may be completed with a pre-filter (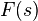 $F(s)$ ) design when it is required. In the case of tracking conditions a shaping on the Bode diagram may be used. Post design analysis is then performed to ensure the system response is satisfactory according with the problem requirements.

The QFT design methodology was originally developed for Single-Input Single-Output (SISO) and Linear Time Invariant Systems (LTI), with the design process being as described above. However, it has since been extended to weakly nonlinear systems, time varying systems, distributed parameter systems, multi-input multi-output (MIMO) systems (Horowitz, 1991), discrete systems (these using the Z-Transform as transfer function), and non minimum phase systems. The development of CAD tools has been an important, more recent development, which simplifies and automates much of the design procedure (Borghesani et al., 1994).

References

Horowitz, I., 1963, Synthesis of Feedback Systems, Academic Press, New York, 1963.
Horowitz, I., and Sidi, M., 1972, “Synthesis of feedback systems with large plant ignorance for prescribed time-domain tolerances,” International Journal of Control, 16(2), pp. 287–309.
Horowitz, I., 1991, “Survey of Quantitative Feedback Theory (QFT),” International Journal of Control, 53(2), pp. 255–291.
Borghesani, C., Chait, Y., and Yaniv, O., 1994, Quantitative Feedback Theory Toolbox Users Guide, The Math Works Inc., Natick, MA.
Zolotas, A. (2005, June 8). QFT - Quantitative Feedback Theory. Connexions.

External links

Mario Garcia-Sanz, Quantitative Robust Control Engineering:Theory and Applications

This article is issued from Wikipedia - version of the 5/3/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.