Quickhull

Quickhull is a method of computing the convex hull of a finite set of points in the plane. It uses a divide and conquer approach similar to that of quicksort, which its name derives from. Its average case complexity is considered to be O(n * log(n)), whereas in the worst case it takes O(n²) (quadratic).

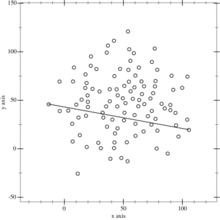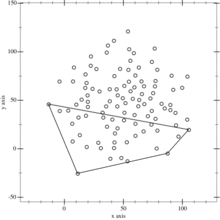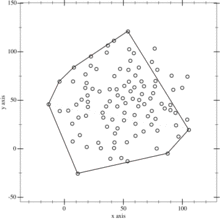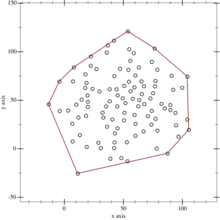
This animation depicts the quickhull algorithm.

Algorithm

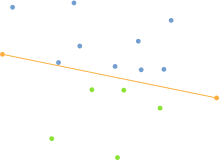
Steps 1-2: Divide points in two subsets

Under average circumstances the algorithm works quite well, but processing usually becomes slow in cases of high symmetry or points lying on the circumference of a circle. The algorithm can be broken down to the following steps:

1. Find the points with minimum and maximum x coordinates, those are bound to be part of the convex hull.
2. Use the line formed by the two points to divide the set in two subsets of points, which will be processed recursively.
3. Determine the point, on one side of the line, with the maximum distance from the line. The two points found before along with this one form a triangle.
4. The points lying inside of that triangle cannot be part of the convex hull and can therefore be ignored in the next steps.
5. Repeat the previous two steps on the two lines formed by the triangle (not the initial line).
6. Keep on doing so on until no more points are left, the recursion has come to an end and the points selected constitute the convex hull.

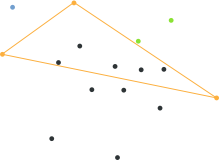
Steps 3-5: Find maximal distance point, ignore points inside triangle and repeat it

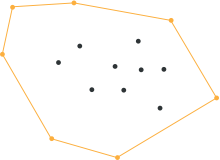
Step 6: Recurse until no more points are left

Pseudo Code

   Input = a set S of n points 
   Assume that there are at least 2 points in the input set S of points
   QuickHull (S) 
   { 
       // Find convex hull from the set S of n points
       Convex Hull := {} 
       Find left and right most points, say A & B, and add A & B to convex hull 
       Segment AB divides the remaining (n-2) points into 2 groups S1 and S2 
           where S1 are points in S that are on the right side of the oriented line from A to B, 
           and S2 are points in S that are on the right side of the oriented line from B to A 
       FindHull (S1, A, B) 
       FindHull (S2, B, A) 
   }
   FindHull (Sk, P, Q) 
   { 
       // Find points on convex hull from the set Sk of points 
       // that are on the right side of the oriented line from P to Q
       If Sk has no point, then return. 
       From the given set of points in Sk, find farthest point, say C, from segment PQ 
       Add point C to convex hull at the location between P and Q 
       Three points P, Q, and C partition the remaining points of Sk into 3 subsets: S0, S1, and S2 
           where S0 are points inside triangle PCQ, S1 are points on the right side of the oriented 
           line from  P to C, and S2 are points on the right side of the oriented line from C to Q. 
       FindHull(S1, P, C) 
       FindHull(S2, C, Q) 
   }
   Output = convex hull

References

• Barber, C. Bradford; Dobkin, David P.; Huhdanpaa, Hannu (1 December 1996). "The quickhull algorithm for convex hulls" (PDF). ACM Transactions on Mathematical Software. 22 (4): 469–483. doi:10.1145/235815.235821. 
• Dave Mount. "Lecture 3: More Convex Hull Algorithms". 
• Pseudocode, "http://www.cse.yorku.ca/~aaw/Hang/quick_hull/Algorithm.html".

External links

• Implementing QuickHull (GDC 2014) – Algorithm presentation with 3D implementation details.