2 21 polytope
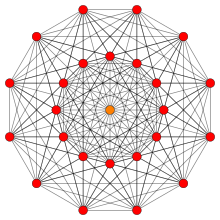 221 |
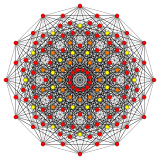 Rectified 221 | |
 (122) |
 Birectified 221 (Rectified 122) | |
| orthogonal projections in E6 Coxeter plane | ||
|---|---|---|
In 6-dimensional geometry, the 221 polytope is a uniform 6-polytope, constructed within the symmetry of the E6 group. It was discovered by Thorold Gosset, published in his 1900 paper. He called it an 6-ic semi-regular figure.[1] It is also called the Schläfli polytope.
Its Coxeter symbol is 221, describing its bifurcating Coxeter-Dynkin diagram, with a single ring on the end of one of the 2-node sequences. He also studied[2] its connection with the 27 lines on the cubic surface, which are naturally in correspondence with the vertices of 221.
The rectified 221 is constructed by points at the mid-edges of the 221. The birectified 221 is constructed by points at the triangle face centers of the 221, and is the same as the rectified 122.
These polytopes are a part of family of 39 convex uniform polytopes in 6-dimensions, made of uniform 5-polytope facets and vertex figures, defined by all permutations of rings in this Coxeter-Dynkin diagram: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
2_21 polytope
| 221 polytope | |
|---|---|
| Type | Uniform 6-polytope |
| Family | k21 polytope |
| Schläfli symbol | {3,3,32,1} |
| Coxeter symbol | 221 |
| Coxeter-Dynkin diagram | |
| 5-faces | 99 total: 27 211 72 {34} |
| 4-faces | 648: 432 {33} 216 {33} |
| Cells | 1080 {3,3} |
| Faces | 720 {3} |
| Edges | 216 |
| Vertices | 27 |
| Vertex figure | 121 (5-demicube) |
| Petrie polygon | Dodecagon |
| Coxeter group | E6, [32,2,1], order 51840 |
| Properties | convex |
The 221 has 27 vertices, and 99 facets: 27 5-orthoplexes and 72 5-simplices. Its vertex figure is a 5-demicube.
For visualization this 6-dimensional polytope is often displayed in a special skewed orthographic projection direction that fits its 27 vertices within a 12-gonal regular polygon (called a Petrie polygon). Its 216 edges are drawn between 2 rings of 12 vertices, and 3 vertices projected into the center. Higher elements (faces, cells, etc.) can also be extracted and drawn on this projection.
The Schläfli graph contains the 1-skeleton of this polytope.
Alternate names
- E. L. Elte named it V27 (for its 27 vertices) in his 1912 listing of semiregular polytopes.[3]
- Icosihepta-heptacontidi-peton - 27-72 facetted polypeton (acronym jak) (Jonathan Bowers)[4]
Coordinates
The 27 vertices can be expressed in 8-space as an edge-figure of the 421 polytope:
- (-2,0,0,0,-2,0,0,0), (0,-2,0,0,-2,0,0,0), (0,0,-2,0,-2,0,0,0), (0,0,0,-2,-2,0,0,0), (0,0,0,0,-2,0,0,-2), (0,0,0,0,0,-2,-2,0)
- (2,0,0,0,-2,0,0,0), (0,2,0,0,-2,0,0,0), (0,0,2,0,-2,0,0,0), (0,0,0,2,-2,0,0,0), (0,0,0,0,-2,0,0,2)
- (-1,-1,-1,-1,-1,-1,-1,-1), (-1,-1,-1, 1,-1,-1,-1, 1), (-1,-1, 1,-1,-1,-1,-1, 1), (-1,-1, 1, 1,-1,-1,-1,-1), (-1, 1,-1,-1,-1,-1,-1, 1), (-1, 1,-1, 1,-1,-1,-1,-1), (-1, 1, 1,-1,-1,-1,-1,-1), (1,-1,-1,-1,-1,-1,-1, 1) (1,-1, 1,-1,-1,-1,-1,-1), (1,-1,-1, 1,-1,-1,-1,-1) (1, 1,-1,-1,-1,-1,-1,-1), (-1, 1, 1, 1,-1,-1,-1, 1) (1,-1, 1, 1,-1,-1,-1, 1) (1, 1,-1, 1,-1,-1,-1, 1) (1, 1, 1,-1,-1,-1,-1, 1) (1, 1, 1, 1,-1,-1,-1,-1)
Construction
Its construction is based on the E6 group.
The facet information can be extracted from its Coxeter-Dynkin diagram, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Removing the node on the short branch leaves the 5-simplex, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Removing the node on the end of the 2-length branch leaves the 5-orthoplex in its alternated form: (211), ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Every simplex facet touches an 5-orthoplex facet, while alternate facets of the orthoplex touch either a simplex or another orthoplex.
The vertex figure is determined by removing the ringed node and ringing the neighboring node. This makes 5-demicube (121 polytope), ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Images
Vertices are colored by their multiplicity in this projection, in progressive order: red, orange, yellow. The number of vertices by color are given in parentheses.
| E6 [12] |
D5 [8] |
D4 / A2 [6] |
B6 [12/2] |
|---|---|---|---|
 (1,3) |
 (1,3) |
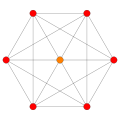 (3,9) |
 (1,3) |
| A5 [6] |
A4 [5] |
A3 / D3 [4] | |
 (1,3) |
 (1,2) |
 (1,4,7) |
Geometric folding
The 221 is related to the 24-cell by a geometric folding of the E6/F4 Coxeter-Dynkin diagrams. This can be seen in the Coxeter plane projections. The 24 vertices of the 24-cell are projected in the same two rings as seen in the 221.
| E6 |
F4 |
 221 |
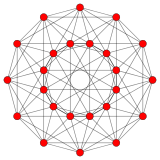 24-cell |
This polytope can tessellate Euclidean 6-space, forming the 222 honeycomb with this Coxeter-Dynkin diagram: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Related complex polyhedra
The regular complex polygon 3{3}3{3}3, ![]()
![]()
![]()
![]()
![]() , in has a real representation as the 221 polytope,
, in has a real representation as the 221 polytope, ![]()
![]()
![]()
![]()
![]()
![]()
![]() , in 4-dimensional space. It is called a Hessian polyhedron after Edmund Hess. It has 27 vertices, 72 3-edges, and 27 3{3}3 faces. Its complex reflection group is 3[3]3[3]3, order 648.
, in 4-dimensional space. It is called a Hessian polyhedron after Edmund Hess. It has 27 vertices, 72 3-edges, and 27 3{3}3 faces. Its complex reflection group is 3[3]3[3]3, order 648.
Related polytopes
The 221 is fourth in a dimensional series of semiregular polytopes. Each progressive uniform polytope is constructed vertex figure of the previous polytope. Thorold Gosset identified this series in 1900 as containing all regular polytope facets, containing all simplexes and orthoplexes.
| k21 figures in n dimensional | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Space | Finite | Euclidean | Hyperbolic | ||||||||
| En | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
| Coxeter group |
E3=A2A1 | E4=A4 | E5=D5 | E6 | E7 | E8 | E9 = = E8+ | E10 = = E8++ | |||
| Coxeter diagram |
|||||||||||
| Symmetry | [3−1,2,1] | [30,2,1] | [31,2,1] | [32,2,1] | [33,2,1] | [34,2,1] | [35,2,1] | [36,2,1] | |||
| Order | 12 | 120 | 192 | 51,840 | 2,903,040 | 696,729,600 | ∞ | ||||
| Graph |  |
 |
 |
 |
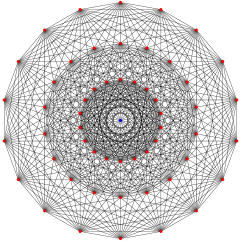 |
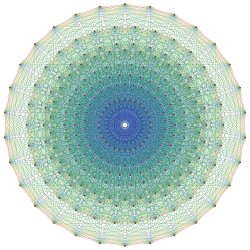 |
- | - | |||
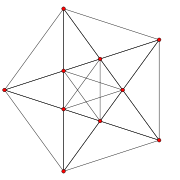
| Name | −121 | 021 | 121 | 221 | 321 | 421 | 521 | 621 | |||
The 221 polytope is fourth in dimensional series 2k2.
| 2k1 figures in n dimensions | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Space | Finite | Euclidean | Hyperbolic | ||||||||
| n | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
| Coxeter group |
E3=A2A1 | E4=A4 | E5=D5 | E6 | E7 | E8 | E9 = = E8+ | E10 = = E8++ | |||
| Coxeter diagram |
|||||||||||
| Symmetry | [3−1,2,1] | [30,2,1] | [[3<sup>1,2,1</sup>]] | [32,2,1] | [33,2,1] | [34,2,1] | [35,2,1] | [36,2,1] | |||
| Order | 12 | 120 | 384 | 51,840 | 2,903,040 | 696,729,600 | ∞ | ||||
| Graph |  |
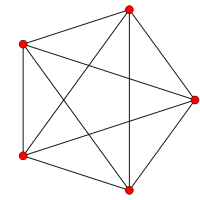 |
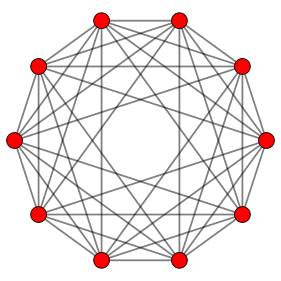 |
 |
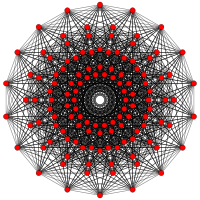 |
 |
- | - | |||
| Name | 2-1,1 | 201 | 211 | 221 | 231 | 241 | 251 | 261 | |||
The 221 polytope is second in dimensional series 22k.
| Space | Finite | Euclidean | Hyperbolic | |
|---|---|---|---|---|
| n | 5 | 6 | 7 | 8 |
| Coxeter group |
A5 | E6 | =E6+ | E6++ |
| Coxeter diagram |
||||
| Graph |  |
 |
∞ | ∞ |
| Name | 220 | 221 | 222 | 223 |
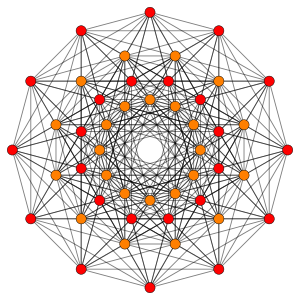
Rectified 2_21 polytope
| Rectified 221 polytope | |
|---|---|
| Type | Uniform 6-polytope |
| Schläfli symbol | t1{3,3,32,1} |
| Coxeter symbol | t1(221) |
| Coxeter-Dynkin diagram | |
| 5-faces | 126 total:
72 t1{34} |
| 4-faces | 1350 |
| Cells | 4320 |
| Faces | 5040 |
| Edges | 2160 |
| Vertices | 216 |
| Vertex figure | rectified 5-cell prism |
| Coxeter group | E6, [32,2,1], order 51840 |
| Properties | convex |
The rectified 221 has 216 vertices, and 126 facets: 72 rectified 5-simplices, and 27 rectified 5-orthoplexes and 27 5-demicubes . Its vertex figure is a rectified 5-cell prism.
Alternate names
- Rectified icosihepta-heptacontidi-peton as a rectified 27-72 facetted polypeton (acronym rojak) (Jonathan Bowers)[5]
Construction
Its construction is based on the E6 group and information can be extracted from the ringed Coxeter-Dynkin diagram representing this polytope: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Removing the ring on the short branch leaves the rectified 5-simplex, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Removing the ring on the end of the other 2-length branch leaves the rectified 5-orthoplex in its alternated form: t1(211), ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Removing the ring on the end of the same 2-length branch leaves the 5-demicube: (121), ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
The vertex figure is determined by removing the ringed ring and ringing the neighboring ring. This makes rectified 5-cell prism, t1{3,3,3}x{}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Images
Vertices are colored by their multiplicity in this projection, in progressive order: red, orange, yellow.
| E6 [12] |
D5 [8] |
D4 / A2 [6] |
B6 [12/2] |
|---|---|---|---|
 |
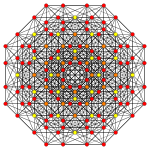 |
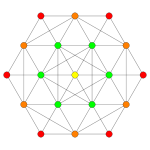 |
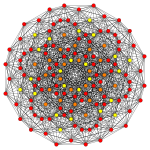 |
| A5 [6] |
A4 [5] |
A3 / D3 [4] | |
 |
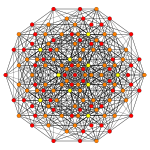 |
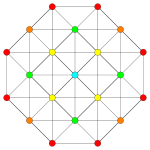 |
See also
Notes
- ↑ Gosset, 1900
- ↑ Coxeter, H.S.M. (1940). "The Polytope 221 Whose Twenty-Seven Vertices Correspond to the Lines on the General Cubic Surface". Amer. J. Math. 62: 457–486. doi:10.2307/2371466. JSTOR 2371466.
- ↑ Elte, 1912
- ↑ Klitzing, (x3o3o3o3o *c3o - jak)
- ↑ Klitzing, (o3x3o3o3o *c3o - rojak)
References
- T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
- Elte, E. L. (1912), The Semiregular Polytopes of the Hyperspaces, Groningen: University of Groningen
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 17) Coxeter, The Evolution of Coxeter-Dynkin diagrams, [Nieuw Archief voor Wiskunde 9 (1991) 233-248] See figure 1: (p. 232) (Node-edge graph of polytope)
- Klitzing, Richard. "6D uniform polytopes (polypeta)". x3o3o3o3o *c3o - jak, o3x3o3o3o *c3o - rojak
| Fundamental convex regular and uniform polytopes in dimensions 2–10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / E9 / E10 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform 4-polytope | 5-cell | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||