Reeb foliation
In mathematics, the Reeb foliation is a particular foliation of the 3-sphere, introduced by the French mathematician Georges Reeb (1920–1992).
It is based on dividing the sphere into two solid tori, along a 2-torus: see Clifford torus. Each of the solid tori is then foliated internally, in codimension 1, and the dividing torus surface forms one more leaf.
By Novikov's compact leaf theorem, every smooth foliation of the 3-sphere includes a compact torus leaf, bounding a solid torus foliated in the same way.
Illustrations
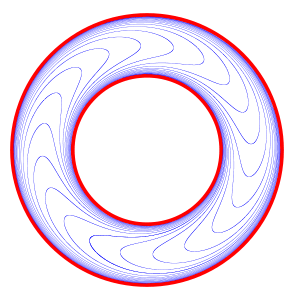 2-dimensional section of Reeb foliation |
 3-dimensional model of Reeb foliation |
References
- G. Reeb (1952). Sur certaines propriétés topologiques des variétés feuillétées. Actualités Sci. Indust. 1183. Paris: Hermann.
- Alberto Candel; Lawrence Conlon (2000). Foliations. American Mathematical Society. p. 93. ISBN 0-8218-0809-5.
- Ieke Moerdijk; J. Mrčun (2003). Introduction to Foliations and Lie Groupoids. Cambridge studies in advanced mathematics. 91. Cambridge University Press. p. 8. ISBN 0-521-83197-0.
External links
This article is issued from Wikipedia - version of the 2/7/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.