Regulated rewriting
Regulated rewriting is a specific area of formal languages studying grammatical systems which are able to take some kind of control over the production applied in a derivation step. For this reason, the grammatical systems studied in Regulated Rewriting theory are also called "Grammars with Controlled Derivations". Among such grammars can be noticed:
Matrix Grammars
Basic concepts
Definition
A Matrix Grammar, 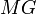 , is a four-tuple
, is a four-tuple 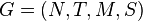 where
where
1.-  is an alphabet of non-terminal symbols
is an alphabet of non-terminal symbols
2.-  is an alphabet of terminal symbols disjoint with
is an alphabet of terminal symbols disjoint with 
3.- 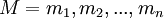 is a finite set of matrices, which are non-empty sequences
is a finite set of matrices, which are non-empty sequences
![m_{i} = [p_{i_1},...,p_{i_{k(i)}}]](../I/m/df884048fc92b15666ce9e37bb43f71f.png) ,
with
,
with 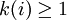 , and
, and
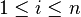 , where each
, where each
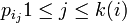 , is an ordered pair
, is an ordered pair
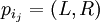 being
being
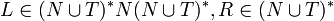 these pairs are called "productions", and are denoted
these pairs are called "productions", and are denoted
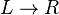 . In these conditions the matrices can be written down as
. In these conditions the matrices can be written down as
![m_i = [L_{i_{1}}\rightarrow R_{i_{1}},...,L_{i_{k(i)}}\rightarrow R_{i_{k(i)}}]](../I/m/366a920c60d8911ffad91dd3e807b3fb.png)
4.- S is the start symbol
Definition
Let 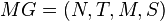 be a matrix grammar and let
be a matrix grammar and let  the collection of all productions on matrices of
the collection of all productions on matrices of  .
We said that
.
We said that 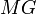 is of type i according to Chomsky's hierarchy with
is of type i according to Chomsky's hierarchy with 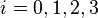 , or "increasing length"
or "linear" or "without
, or "increasing length"
or "linear" or "without 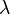 -productions" if and only if the grammar
-productions" if and only if the grammar 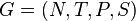 has the corresponding property.
has the corresponding property.
The classic example
- Note: taken from Abraham 1965, with change of nonterminals names
The context-sensitive language
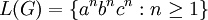 is generated by the
is generated by the 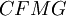
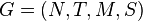 where
where
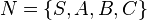 is the non-terminal set,
is the non-terminal set,
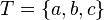 is the terminal set,
and the set of matrices is defined as
is the terminal set,
and the set of matrices is defined as
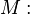
![\left[S\rightarrow abc\right]](../I/m/f97e777419cbea6343cfa24e0c08802d.png) ,
,
![\left[S\rightarrow aAbBcC\right]](../I/m/902361db2ad2452c7cf616750de3caa9.png) ,
,
![\left[A\rightarrow aA,B\rightarrow bB,C\rightarrow cC\right]](../I/m/6ab913107364f152dd85e5dd02fbea57.png) ,
,
![\left[A\rightarrow a,B\rightarrow b,C\rightarrow c\right]](../I/m/4bcefde2fc4228c2d29a3ed98d9b4c11.png) .
.
Time Variant Grammars
Basic concepts
Definition
A Time Variant Grammar is a pair 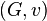 where
where 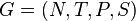 is a grammar and
is a grammar and 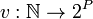 is a function from the set of natural
numbers to the class of subsets of the set of productions.
is a function from the set of natural
numbers to the class of subsets of the set of productions.
Programmed Grammars
Basic concepts
Definition
A Programmed Grammar is a pair 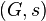 where
where 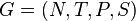 is a grammar and
is a grammar and 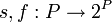 are the success and fail functions from the set of productions
to the class of subsets of the set of productions.
are the success and fail functions from the set of productions
to the class of subsets of the set of productions.
Grammars with regular control language
Basic concepts
Definition
A Grammar With Regular Control Language,
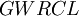 , is a pair
, is a pair 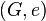 where
where 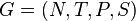 is a grammar and
is a grammar and  is a regular expression over the alphabet of the set of productions.
is a regular expression over the alphabet of the set of productions.
A naive example
Consider the CFG
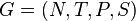 where
where
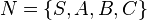 is the non-terminal set,
is the non-terminal set,
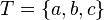 is the terminal set,
and the productions set is defined as
is the terminal set,
and the productions set is defined as
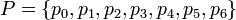 being
being
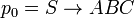
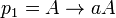 ,
,
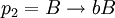 ,
,
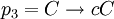
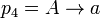 ,
,
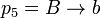 , and
, and
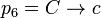 .
Clearly,
.
Clearly,
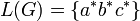 .
Now, considering the productions set
.
Now, considering the productions set
 as an alphabet (since it is a finite set),
define the regular expression over
as an alphabet (since it is a finite set),
define the regular expression over 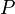 :
:
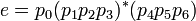 .
.
Combining the CFG grammar 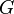 and the regular expression
and the regular expression
 , we obtain the CFGWRCL
, we obtain the CFGWRCL
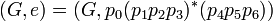 which generates the language
which generates the language
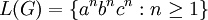 .
.
Besides there are other grammars with regulated rewriting, the four cited above are good examples of how to extend context-free grammars with some kind of control mechanism to obtain a Turing machine powerful grammatical device.
Sources
[1] Salomaa, Arto (1973) Formal languages Academic Press, ACM monograph series
[2] Rozenberg, G.; Salomaa, A. (eds.) 1997 Handbook of formal languages Berlin; New York : Springer ISBN 3-540-61486-9 (set) (3540604200 : v. 1; 3540606483 : v. 2; 3540606491: v. 3)
[3] Dassow, Jurgen; Paun, G. 1990 Regulated Rewriting in Formal Language Theory ISBN 0387514147. Springer-Verlag New York, Inc. Secaucus, NJ, USA Pages: 308. Medium: Hardcover.
[4] Dassow, Jurgen; von-Guericke, Otto Grammars with Regulated Rewriting Available at: and ()
[5] Abraham, S. 1965. "Some questions of language theory", Proceedings of the 1965 International Conference On Computational Linguistics, pp 1 – 11, Bonn, Germany Available at: