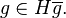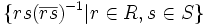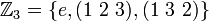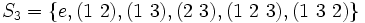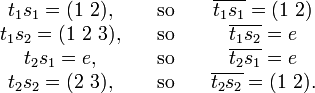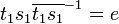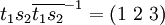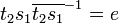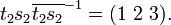Schreier's lemma

In mathematics, Schreier's lemma is a theorem in group theory used in the Schreier–Sims algorithm and also for finding a presentation of a subgroup.

Definition

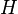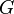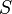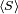Suppose $H$ is a subgroup of $G$ , which is finitely generated with generating set $S$ , that is, G = $\scriptstyle \langle S\rangle$ .

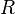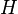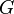Let $R$ be a right transversal of $H$ in $G$ . In other words, 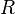$R$ is (the image of) a section of the quotient map 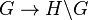$G \to H\backslash G$ , where 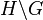$H\backslash G$ denotes the set of right cosets of 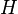$H$ in $G$ .

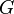We make the definition that given 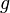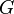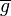$g$ ∈ $G$ , $\overline{g}$ is the chosen representative in the transversal 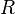$R$ of the coset 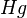$Hg$ , that is,

g\in H\overline{g}.

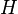Then $H$ is generated by the set

\{rs(\overline{rs})^{-1}|r\in R, s\in S\}

Example

Let us establish the evident fact that the group Z₃ = Z/3Z is indeed cyclic. Via Cayley's theorem, Z₃ is a subgroup of the symmetric group S₃. Now,

\Bbb{Z}_3=\{ e, (1\ 2\ 3), (1\ 3\ 2) \}

S_3= \{ e, (1\ 2), (1\ 3), (2\ 3), (1\ 2\ 3), (1\ 3\ 2) \}

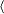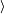where $e$ is the identity permutation. Note S₃ = $\scriptstyle\langle$ { s₁=(1 2), s₂ = (1 2 3) } $\scriptstyle\rangle$ .

Z₃ has just two cosets, Z₃ and S₃ \ Z₃, so we select the transversal { t₁ = e, t₂=(1 2) }, and we have

\begin{matrix} t_1s_1 = (1\ 2),&\quad\text{so}\quad&\overline{t_1s_1} = (1\ 2)\\ t_1s_2 = (1\ 2\ 3) ,&\quad\text{so}\quad& \overline{t_1s_2} = e\\ t_2s_1 = e ,&\quad\text{so}\quad& \overline{t_2s_1} = e\\ t_2s_2 = (2\ 3) ,&\quad\text{so}\quad& \overline{t_2s_2} = (1\ 2). \\ \end{matrix}

Finally,

t_1s_1\overline{t_1s_1}^{-1} = e

t_1s_2\overline{t_1s_2}^{-1} = (1\ 2\ 3)

t_2s_1\overline{t_2s_1}^{-1} = e

t_2s_2\overline{t_2s_2}^{-1} = (1\ 2\ 3).

Thus, by Schreier's subgroup lemma, { e, (1 2 3) } generates Z₃, but having the identity in the generating set is redundant, so we can remove it to obtain another generating set for Z₃, { (1 2 3) } (as expected).

References

Seress, A. Permutation Group Algorithms. Cambridge University Press, 2002.

This article is issued from Wikipedia - version of the 9/7/2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.