Smoothstep

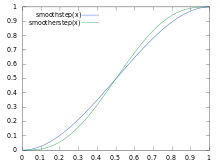
A plot of the smoothstep(x) and smootherstep(x) functions, using 0 as the left edge and 1 as the right edge.

Smoothstep is an interpolation function commonly used in computer graphics^[1]^[2] and video game engines.^[3]

The function depends on two parameters, the "left edge" and the "right edge", with the left edge being assumed smaller than the right edge. The function takes a real number x as input and outputs 0 if x is less than or equal to the left edge, 1 if x is greater than or equal to the right edge, and smoothly interpolates between 0 and 1 otherwise. The slope of the smoothstep function is zero at both edges. This makes it easy to create a sequence of transitions using smoothstep to interpolate each segment rather than using a more sophisticated or expensive interpolation technique.

As pointed out in MSDN and OpenGL documentation, smoothstep implements cubic Hermite interpolation after doing a clamp:

\operatorname {smoothstep} (x)=3x^{2}-2x^{3}

where we assume that the left edge is 0, the right edge is 1, and 0 ≤ x ≤ 1.

A C/C++ example implementation provided by AMD^[4] follows.

float smoothstep(float edge0, float edge1, float x)
{
    // Scale, bias and saturate x to 0..1 range
    x = clamp((x - edge0)/(edge1 - edge0), 0.0, 1.0); 
    // Evaluate polynomial
    return x*x*(3 - 2*x);
}

Variations

Ken Perlin suggests^[5] an improved version of the smoothstep function which has zero 1st and 2nd order derivatives at x=0 and x=1:

\operatorname {smootherstep} (x)=6x^{5}-15x^{4}+10x^{3}

C/C++ reference implementation:

float smootherstep(float edge0, float edge1, float x)
{
    // Scale, and clamp x to 0..1 range
    x = clamp((x - edge0)/(edge1 - edge0), 0.0, 1.0);
    // Evaluate polynomial
    return x*x*x*(x*(x*6 - 15) + 10);
}

Origin

3rd order equation

We start with a generic third order polynomial function and its first derivative:

{\begin{alignedat}{9}f(x)&&\;=\;&&a_{3}x^{3}&&\;+\;&&a_{2}x^{2}&&\;+\;&&a_{1}x&&\;+\;&&a_{0}&\\f'(x)&&\;=\;&&3a_{3}x^{2}&&\;+\;&&2a_{2}x&&\;+\;&&a_{1}&\end{alignedat}}

Applying the desired values for the function at both endpoints we get:

{\begin{alignedat}{13}f(0)&&\;=\;&&0\;\;\;\;\;&&\Rightarrow &&\;\;\;\;\;0\;&&+&&\;0\;&&+&&\;0\;&&+&&\;a_{0}&&\;=\;&&0&\\f(1)&&\;=\;&&1\;\;\;\;\;&&\Rightarrow &&\;\;\;\;\;a_{3}\;&&+&&\;a_{2}\;&&+&&\;a_{1}\;&&+&&\;a_{0}&&\;=\;&&1&\end{alignedat}}

Applying the desired values for the first derivative of the function at both endpoints we get:

{\begin{alignedat}{11}f'(0)&&\;=\;&&0\;\;\;\;&&\Rightarrow &&\;\;\;\;0\;&&+&&\;0\;&&+&&\;a_{1}\;&&=\;&&0&\\f'(1)&&\;=\;&&0\;\;\;\;&&\Rightarrow &&\;\;\;\;3a_{3}\;&&+&&\;2a_{2}\;&&+&&\;a_{1}\;&&=\;&&0&\end{alignedat}}

Solving the system of 4 unknowns formed by the last 4 equations we obtain the values of the polynomial coefficients:

a_{0}=0,\;\;\;\;\;\;a_{1}=0,\;\;\;\;\;\;a_{2}=3,\;\;\;\;\;\;a_{3}=-2

Introducing these coefficients back into the first equation gives the third order smoothstep function:

f(x)=-2x^{3}+3x^{2}

5th order equation

We start with a generic fifth order polynomial function, its first derivative and its second derivative:

{\begin{alignedat}{13}f(x)&&\;=\;&&a_{5}x^{5}&&\;+\;&&a_{4}x^{4}&&\;+\;&&a_{3}x^{3}&&\;+\;&&a_{2}x^{2}&&\;+\;&&a_{1}x&&\;+\;&&a_{0}&\\f'(x)&&\;=\;&&5a_{5}x^{4}&&\;+\;&&4a_{4}x^{3}&&\;+\;&&3a_{3}x^{2}&&\;+\;&&2a_{2}x&&\;+\;&&a_{1}&\\f''(x)&&\;=\;&&20a_{5}x^{3}&&\;+\;&&12a_{4}x^{2}&&\;+\;&&6a_{3}x&&\;+\;&&2a_{2}&\end{alignedat}}

Applying the desired values for the function at both endpoints we get:

{\begin{alignedat}{17}f(0)&&\;=\;&&0\;\;\;\;\;&&\Rightarrow &&\;\;\;\;\;0\;&&+&&\;0\;&&+&&\;0\;&&+&&\;0\;&&+&&\;0\;&&+&&\;a_{0}&&\;=\;&&0&\\f(1)&&\;=\;&&1\;\;\;\;\;&&\Rightarrow &&\;\;\;\;\;a_{5}\;&&+&&\;a_{4}\;&&+&&\;a_{3}\;&&+&&\;a_{2}\;&&+&&\;a_{1}\;&&+&&\;a_{0}&&\;=\;&&1&\end{alignedat}}

Applying the desired values for the first derivative of the function at both endpoints we get:

{\begin{alignedat}{15}f'(0)&&\;=\;&&0\;\;\;\;&&\Rightarrow &&\;\;\;\;0\;&&+&&\;0\;&&+&&\;0\;&&+&&\;0\;&&+&&\;a_{1}\;&&=\;&&0&\\f'(1)&&\;=\;&&0\;\;\;\;&&\Rightarrow &&\;\;\;\;5a_{5}\;&&+&&\;4a_{4}\;&&+&&\;3a_{3}\;&&+&&\;2a_{2}\;&&+&&\;a_{1}\;&&=\;&&0&\end{alignedat}}

Applying the desired values for the second derivative of the function at both endpoints we get:

{\begin{alignedat}{15}f''(0)&&\;=\;&&0\;\;\;\;&&\Rightarrow &&\;\;\;\;0\;&&+&&\;0\;&&+&&\;0\;&&+&&\;2a_{2}\;&&=\;&&0&\\f''(1)&&\;=\;&&0\;\;\;\;&&\Rightarrow &&\;\;\;\;20a_{5}\;&&+&&\;12a_{4}\;&&+&&\;6a_{3}\;&&+&&\;2a_{2}\;&&=\;&&0&\end{alignedat}}

Solving the system of 6 unknowns formed by the last 6 equations we obtain the values of the polynomial coefficients:

a_{0}=0,\;\;\;\;\;\;a_{1}=0,\;\;\;\;\;\;a_{2}=0,\;\;\;\;\;\;a_{3}=10,\;\;\;\;\;\;a_{4}=-15,\;\;\;\;\;\;a_{5}=6

Introducing these coefficients back into the first equation gives the fifth order smootherstep function:

f(x)=6x^{5}-15x^{4}+10x^{3}

7th order equation

Also called "smootheststep", the 7th order equation was derived by Kyle McDonald and first posted to Twitter^[6] with a derivation on GitHub:^[7]

f(x)=-20x^{7}+70x^{6}-84x^{5}+35x^{4}

Generalization of higher-order equations

All smoothstep equations can be generalized as:

\operatorname {S} _{a}(x)=\sum _{n=0}^{a-1}{\binom {-a}{n}}{\binom {2a-1}{a-n-1}}x^{a+n}

where a determines the order of the resulting polynomial equation, with the order being calculated as 2a - 1. Evaluating this function for different values of a gives:

\operatorname {S} _{1}(x)=x

\operatorname {S} _{2}(x)=-2x^{3}+3x^{2}

\operatorname {S} _{3}(x)=6x^{5}-15x^{4}+10x^{3}

\operatorname {S} _{4}(x)=-20x^{7}+70x^{6}-84x^{5}+35x^{4}

\operatorname {S} _{5}(x)=70x^{9}-315x^{8}+540x^{7}-420x^{6}+126x^{5}

For any value a where a > 0, this generalization will smoothly interpolate from 0 to 1 for any value x on the interval 0 ≤ x ≤ 1 while retaining the property S_a(0.5) = 0.5.

References

↑ Smoothstep at Microsoft Developer Network
↑ GLSL Language Specification, Version 1.40
↑ Unity game engine SmoothStep documentation
↑ ATI R3x0 Pixel Shaders
↑ Texturing and Modeling, Third Edition: A Procedural Approach
↑ kcimc (25 March 2015). "smootheststep(t)=-20*t^7+70*t^6-84*t^5+35*t^4 // when smootherstep's second derivative isn't enough" (Tweet) – via Twitter.
↑ Kyle McDonald (27 March 2015). "Derivation of 7th-order smoothstep function with zeros in third derivative.". Github.com. Retrieved 20 December 2015.

External links

Using smoothstep (in the RenderMan Shading Language) by Prof. Malcolm Kesson.
Interpolation tricks by Jari Komppa
Swift Interpolation Playground demonstrates smoothStep(), smootherStep() and smoothestStep() in a Swift playground by Simon Gladman

This article is issued from Wikipedia - version of the 10/10/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.