Squire's theorem

In fluid dynamics, Squire's theorem states that of all the perturbations that may be applied to a shear flow (i.e. a velocity field of the form 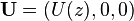), the perturbations which are least stable are two-dimensional, i.e. of the form 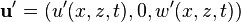.^[1] This applies to incompressible flows which are governed by the Navier–Stokes equations.

Squire's theorem allows many simplifications to be made in stability theory. If we want to decide whether a flow is unstable or not, it suffices to look at two-dimensional perturbations. These are governed by the Orr–Sommerfeld equation.

References