Orthogonal symmetric Lie algebra

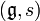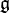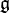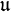In mathematics, an orthogonal symmetric Lie algebra is a pair $(\mathfrak{g}, s)$ consisting of a real Lie algebra $\mathfrak{g}$ and an automorphism $s$ of $\mathfrak{g}$ of order $2$ such that the eigenspace $\mathfrak{u}$ of s corrsponding to 1 (i.e., the set 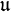$\mathfrak{u}$ of fixed points) is a compact subalgebra. If "compactness" is omitted, it is called a symmetric Lie algebra. An orthogonal symmetric Lie algebra is said to be effective if 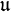$\mathfrak{u}$ intersects the center of 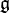$\mathfrak{g}$ trivially. In practice, effectiveness is often assumed; we do this in this article as well.

The canonical example is the Lie algebra of a symmetric space, $s$ being the differential of a symmetry.

Every orthogonal symmetric Lie algebra decomposes into a direct sum of ideals "of compact type", "of noncompact type" and "of Euclidean type".

References

S. Helgason, Differential geometry, Lie groups, and symmetric spaces

This article is issued from Wikipedia - version of the 3/5/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.