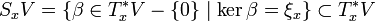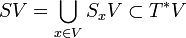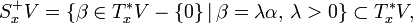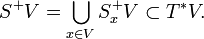Symplectization
In mathematics, the symplectization of a contact manifold is a symplectic manifold which naturally corresponds to it.
Definition
Let 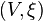 be a contact manifold, and let
be a contact manifold, and let 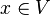 . Consider the set
. Consider the set
of all nonzero 1-forms at 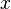 , which have the contact plane
, which have the contact plane 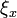 as their kernel. The union
as their kernel. The union
is a symplectic submanifold of the cotangent bundle of 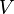 , and thus possesses a natural symplectic structure.
, and thus possesses a natural symplectic structure.
The projection 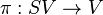 supplies the symplectization with the structure of a principal bundle over
supplies the symplectization with the structure of a principal bundle over 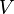 with structure group
with structure group  .
.
The coorientable case
When the contact structure 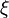 is cooriented by means of a contact form
is cooriented by means of a contact form  , there is another version of symplectization, in which only forms giving the same coorientation to
, there is another version of symplectization, in which only forms giving the same coorientation to 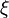 as
as  are considered:
are considered:
Note that 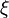 is coorientable if and only if the bundle
is coorientable if and only if the bundle 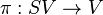 is trivial. Any section of this bundle is a coorienting form for the contact structure.
is trivial. Any section of this bundle is a coorienting form for the contact structure.