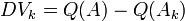Term Discrimination

Term Discrimination is a way to rank keywords in how useful they are for information retrieval.

Overview

This is a method similar to tf-idf but it deals with finding keywords suitable for information retrieval and ones that are not. Please refer to Vector Space Model first.

This method uses the concept of Vector Space Density that the less dense an occurrence matrix is, the better an information retrieval query will be.

An optimal index term is one that can distinguish two different documents from each other and relate two similar documents. On the other hand, a sub-optimal index term can not distinguish two different document from two similar documents.

The discrimination value is the difference in the occurrence matrix's vector-space density versus the same matrix's vector-space without the index term's density.

Let:
 $A$  be the occurrence matrix
 $A_k$  be the occurrence matrix without the index term  $k$ 
and  $Q(A)$  be density of  $A$ .
Then:
The discrimination value of the index term  $k$  is: 
 $DV_k = Q(A) - Q(A_k)$

How to compute

Given an occurrency matrix: 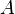$A$ and one keyword: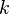 $k$

Find the global document centroid: 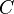$C$ (this is just the average document vector)
Find the average euclidean distance from every document vector, 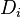$D_i$ to $C$
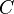
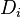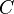Find the average euclidean distance from every document vector, $D_i$ to $C$ IGNORING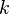 $k$
The difference between the two values in the above step is the discrimination value for keyword $K$

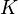
A higher value is better because including the keyword will result in better information retrieval.

Qualitative Observations

Keywords that are sparse should be poor discriminators because they have poor recall, whereas keywords that are frequent should be poor discriminators because they have poor precision.

References

G. Salton, A. Wong, and C. S. Yang (1975), "A Vector Space Model for Automatic Indexing," Communications of the ACM, vol. 18, nr. 11, pages 613–620. (The article in which the vector space model was first presented)
Can, F., Ozkarahan, E. A (1987), "Computation of term/document discrimination values by use of the cover coefficient concept." Journal of the American Society for Information Science, vol. 38, nr. 3, pages 171-183.

This article is issued from Wikipedia - version of the 3/29/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.