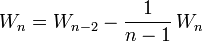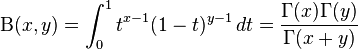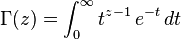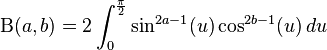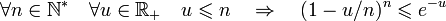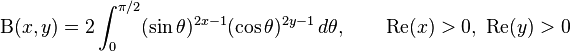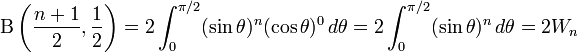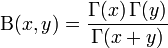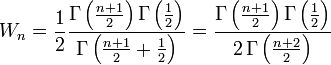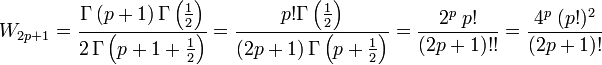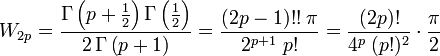Wallis' integrals
In mathematics, and more precisely in analysis, the Wallis' integrals constitute a family of integrals introduced by John Wallis.
Definition, basic properties
The Wallis' integrals are the terms of the sequence
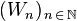 defined by:
defined by:
or equivalently (through a substitution: 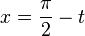 ):
):
In particular, the first few terms of this sequence are:
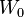 |
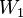 |
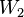 |
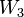 |
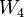 |
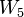 |
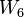 |
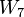 |
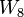 |
... |
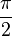 |
 |
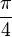 |
 |
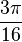 |
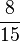 |
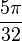 |
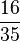 |
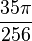 |
... |
The sequence 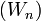 is decreasing and has strictly positive terms.
In fact, for all
is decreasing and has strictly positive terms.
In fact, for all 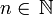 :
:
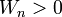 , because it is an integral of a non-negative continuous function which is not all zero in the integration interval
, because it is an integral of a non-negative continuous function which is not all zero in the integration interval![W_{n} - W_{n + 1}= \int_0^{\frac{\pi}{2}} \sin^{n}(x)\,dx - \int_0^{\frac{\pi}{2}} \sin^{n + 1}(x)\,dx = \int_0^{\frac{\pi}{2}} \sin^{n}(x)\, [1 - \sin(x)]\,dx \geqslant 0](../I/m/39e8bbdc24b6328a62ccec12a20f9e69.png)
- (by the linearity of integration and because the last integral is an integral of a non-negative function within the integration interval)
Note: Since the sequence 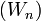 is decreasing and bounded below by 0, it converges to a non-negative limit. Indeed, the limit is zero (see below).
is decreasing and bounded below by 0, it converges to a non-negative limit. Indeed, the limit is zero (see below).
Recurrence relation, evaluating the Wallis' integrals
By means of integration by parts, an interesting recurrence relation can be obtained:
- Noting that for all real
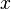 ,
, 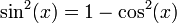 , we have, for all natural numbers
, we have, for all natural numbers 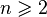 ,
,
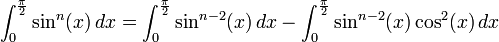 (equation
(equation 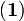 )
)
Integrating the second integral by parts, with:
-
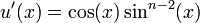 , whose anti-derivative is
, whose anti-derivative is 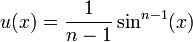
-
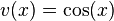 , whose derivative is
, whose derivative is 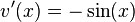
-
we have:
Substituting this result into 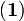 gives:
gives:
and thus
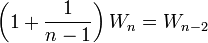 (equation
(equation 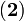 )
)
This gives the well-known identity:
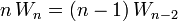 , valid for all
, valid for all 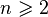 .
.
This is a recurrence relation giving 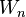 in terms of
in terms of 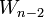 .
This, together with the values of
.
This, together with the values of 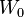 and
and 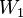 ,
give us two sets of formulae for the terms in the sequence
,
give us two sets of formulae for the terms in the sequence 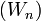 ,
depending on whether
,
depending on whether 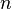 is odd or even.
is odd or even.
- for
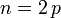 ,
, 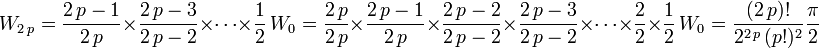
- for
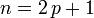 ,
, 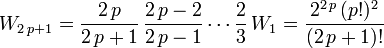
Note that all the even terms are irrational, whereas the odd terms are all rational.
Another relation to evaluate the Wallis' integrals
Wallis's integrals can be evaluated by using Euler integral :
- Euler integral of the first kind: the Beta function:
- Euler integral of the second kind: the Gamma function:
If we make the following substitution inside the Beta function:
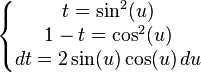
We obtain :
We know that 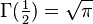 , so this gives us the following relation to evaluate the Wallis'integrals:
, so this gives us the following relation to evaluate the Wallis'integrals:
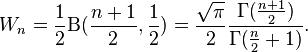
Equivalence
- From the recurrence formula above
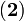 , we can deduce that
, we can deduce that
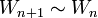 (equivalence of two sequences).
(equivalence of two sequences).
- Indeed, for all
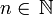 :
: 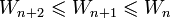 (since the sequence is decreasing)
(since the sequence is decreasing)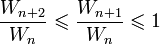 (since
(since 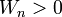 )
)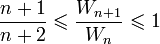 (by equation
(by equation  ).
).- By the sandwich theorem, we conclude that
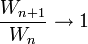 , and hence
, and hence 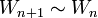 .
.
- By examining
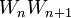 , one obtains the following equivalence:
, one obtains the following equivalence:
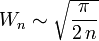 ( and consequently
( and consequently 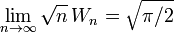 ).
).
For all 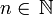 , let
, let 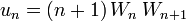 .
.
It turns out that, 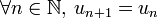 because of equation
because of equation 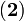 .
In other words
.
In other words 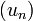 is a constant.
is a constant.
It follows that for all 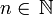 ,
,
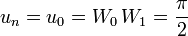 .
.
Now, since 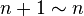 and
and 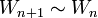 , we have, by the product rules of equivalents,
, we have, by the product rules of equivalents, 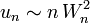 .
.
Thus, 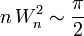 ,
from which the desired result follows
(noting that
,
from which the desired result follows
(noting that 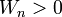 ).
).
Deducing Stirling's formula
Suppose that we have the following equivalence (known as Stirling's formula)
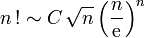 , where
, where 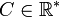 .
.
We now want to determine the value of this constant 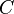 using the formula for
using the formula for 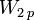 .
.
- From above, we know that:
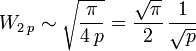 (equation
(equation 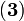 )
)
- Expanding
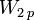 and using the formula above for the factorials, we get:
and using the formula above for the factorials, we get:
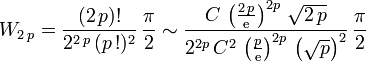 and hence:
and hence: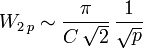 (equation
(equation  )
)- From
 and
and 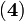 , we obtain, by transitivity,
, we obtain, by transitivity, 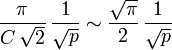 , which gives :
, which gives :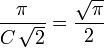 , and hence
, and hence 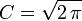 .
.
- We have thus proved Stirling's formula:
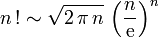 .
.
Evaluating the Gaussian Integral
The Gaussian integral can be evaluated through the use of Wallis' integrals.
We first prove the following inequalities:
In fact, letting 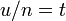 ,
the first inequality (in which
,
the first inequality (in which ![t \in [0,1]](../I/m/d9a06fde4663cdd5b1ba693e9127232f.png) ) is
equivalent to
) is
equivalent to 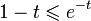 ;
whereas the second inequality reduces to
;
whereas the second inequality reduces to
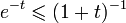 ,
which becomes
,
which becomes 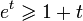 .
These 2 latter inequalities follow from the convexity of the
exponential function
(or from an analysis of the function
.
These 2 latter inequalities follow from the convexity of the
exponential function
(or from an analysis of the function 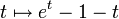 ).
).
Letting 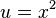 and
making use of the basic properties of improper integrals
(the convergence of the integrals is obvious),
we obtain the inequalities:
and
making use of the basic properties of improper integrals
(the convergence of the integrals is obvious),
we obtain the inequalities:
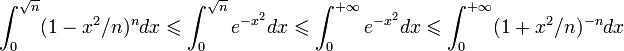 for use with the sandwich theorem (as
for use with the sandwich theorem (as 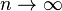 ).
).
The first and last integrals can be evaluated easily using
Wallis' integrals.
For the first one, let 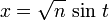 (t varying from 0 to
(t varying from 0 to 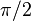 ).
Then, the integral becomes
).
Then, the integral becomes 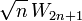 .
For the last integral, let
.
For the last integral, let 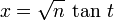 (t varying from
(t varying from 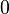 to
to 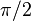 ).
Then, it becomes
).
Then, it becomes 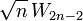 .
.
As we have shown before,
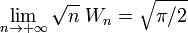 . So, it follows that
. So, it follows that
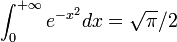 .
.
Remark: There are other methods of evaluating the Gaussian integral. Some of them are more direct.
Relation with the Beta and Gamma functions
One of the definitions of the Beta function reads:
Putting 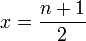 ,
, 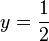 into this equation gives us an expression of the Wallis' integrals in terms of the Beta function:
into this equation gives us an expression of the Wallis' integrals in terms of the Beta function:
or equivalently,
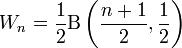 .
.
Exploiting the identity relating the Beta function to Gamma function:
We can rewrite the above in terms of the Gamma function:
So, for odd 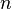 , writing
, writing 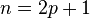 , we have:
, we have:
whereas for even 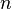 , writing
, writing 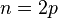 , we get:
, we get:
Note
The same properties lead to Wallis product,
which expresses 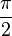 (see
(see 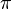 )
in the form of an infinite product.
)
in the form of an infinite product.
External links
- Pascal Sebah and Xavier Gourdon. Introduction to the Gamma Function. In PostScript and HTML formats.
| ||||||||||||||
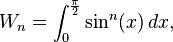
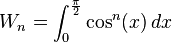
![\int_0^{\frac{\pi}{2}} \sin^{n}(x)\,dx = \int_0^{\frac{\pi}{2}} \sin^{n-2}(x) \left[1-\cos^2(x)\right]\,dx](../I/m/98c0b7d9393d81dcab90fa76142d0fe2.png)
![\int_0^{\frac{\pi}{2}} \sin^{n-2}(x) \cos^2(x)\,dx = \left[ \frac{1}{n-1} \sin^{n-1}(x) \cos(x)\right]_0^{\frac{\pi}{2}} + \int_0^{\frac{\pi}{2}} \ \frac{1}{n-1} \sin^{n-1}(x) \sin(x)\,dx = 0 + {1\over {n-1}}\,W_{n}](../I/m/43a583d5bbf58b040a0cf4d7f9926f7a.png)