Wittgenstein's rod
Wittgenstein's rod is a geometry problem discussed by 20th century philosopher Ludwig Wittgenstein.
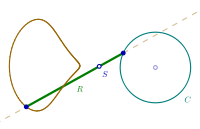
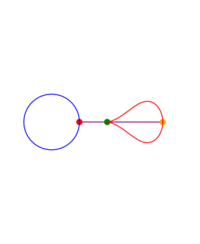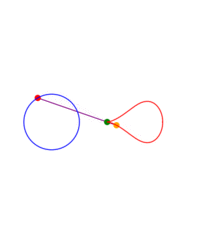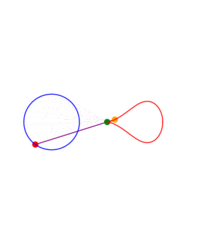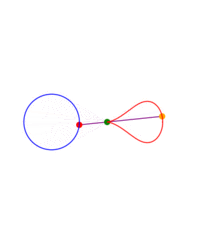
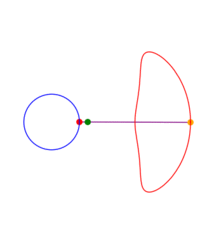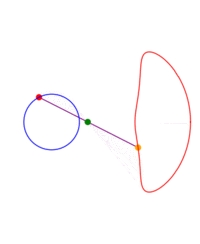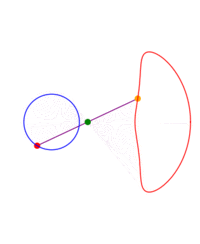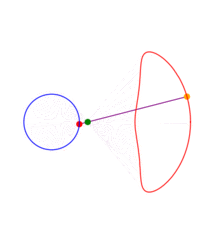
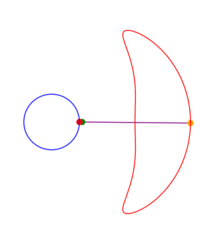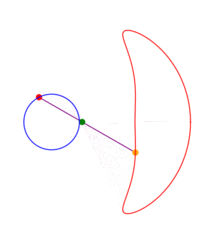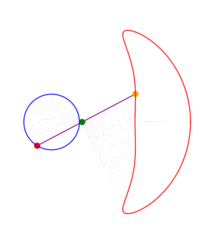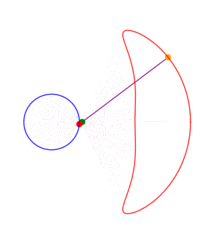
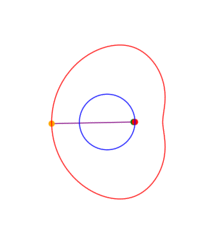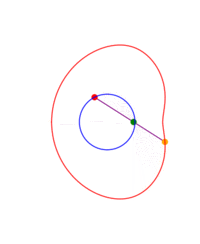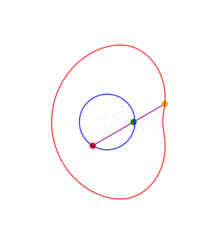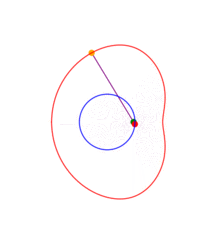
A ray is drawn with its origin 'A' on a circle, through an external point S and a point B is chosen at some constant distance from the starting end of the ray; what figure does B describe when all the initial points on the circle are considered? The answer depends on three parameters: the radius of the circle, the distance from the center to S and the length of the segment AB. The shape described by B can be seen as a 'figure of eight' which in some cases degenerates to a single lobe looking like an inverted cardioid.
If B remains on the same side of S with respect to the center of the circle, instead of a ray one can consider just a segment or the rod 'AB'.
Wittgenstein sketched a mechanism and wrote:
While the point A describes a circle, B describes a figure eight. Now we write this down as a proposition of kinematics.When I work the mechanism its movement proves the proposition to me; as would a construction on paper. The proposition corresponds e.g. to a picture of the mechanism with the paths of the points A and B drawn in. Thus it is in a certain respect a picture of that movement. It holds fast what the proof shows me. Or - what it persuades me of.
This text has been included among the notes selected for publication in Remarks on the Foundations of Mathematics and the editors have dated in the as spring of 1944.[1]
Animations
References
- ↑ Wittgenstein L., Remarks on the Foundations of Mathematics, edited by G.H. von Wright and Rush Rhees, Oxford: Blackwell 1998, ISBN 0-631-12505-1, sect V, §72, p.434