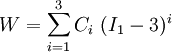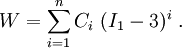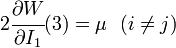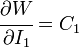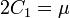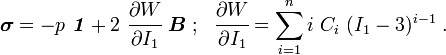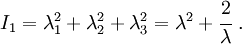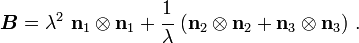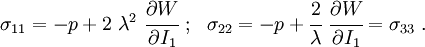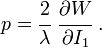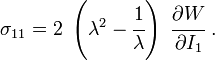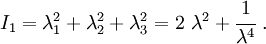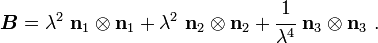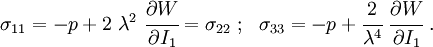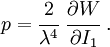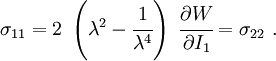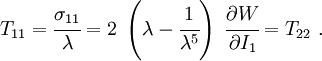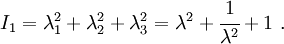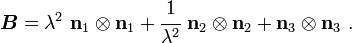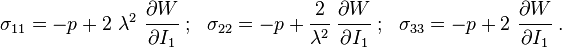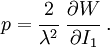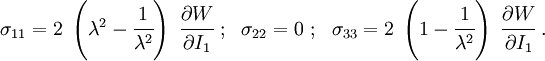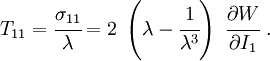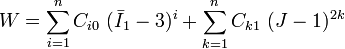Yeoh (hyperelastic model)

Yeoh model prediction versus experimental data for natural rubber. Model parameters and experimental data from PolymerFEM.com

The Yeoh hyperelastic material model[1] is a phenomenological model for the deformation of nearly incompressible, nonlinear elastic materials such as rubber. The model is based on Ronald Rivlin's observation that the elastic properties of rubber may be described using a strain energy density function which is a power series in the strain invariants 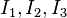I_1, I_2, I_3.[2] The Yeoh model for incompressible rubber is a function only of 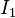I_1. For compressible rubbers, a dependence on 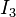I_3 is added on. Since a polynomial form of the strain energy density function is used but all the three invariants of the left Cauchy-Green deformation tensor are not, the Yeoh model is also called the reduced polynomial model.

Yeoh model for incompressible rubbers

Strain energy density function

The original model proposed by Yeoh had a cubic form with only I_1 dependence and is applicable to purely incompressible materials. The strain energy density for this model is written as

W = \sum_{i=1}^3 C_i~(I_1-3)^i

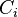where C_i are material constants. The quantity 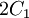2 C_1 can be interpreted as the initial shear modulus.

Today a slightly more generalized version of the Yeoh model is used.[3] This model includes 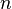n terms and is written as

W = \sum_{i=1}^n C_i~(I_1-3)^i ~.

When n=1 the Yeoh model reduces to the neo-Hookean model for incompressible materials.

For consistency with linear elasticity the Yeoh model has to satisfy the condition

2\cfrac{\partial W}{\partial I_1}(3) = \mu ~~(i \ne j)

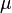where \mu is the shear modulus of the material. Now, at I_1 = 3 (\lambda_i = \lambda_j = 1),

\cfrac{\partial W}{\partial I_1} = C_1

Therefore, the consistency condition for the Yeoh model is

2C_1 = \mu\,

Stress-deformation relations

The Cauchy stress for the incompressible Yeoh model is given by

\boldsymbol{\sigma} = -p~\boldsymbol{\mathit{1}} + 2~\cfrac{\partial W}{\partial I_1}~\boldsymbol{B} ~;~~ \cfrac{\partial W}{\partial I_1} = \sum_{i=1}^n i~C_i~(I_1-3)^{i-1} ~.

Uniaxial extension

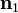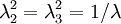For uniaxial extension in the \mathbf{n}_1-direction, the principal stretches are \lambda_1 = \lambda,~ \lambda_2=\lambda_3. From incompressibility \lambda_1~\lambda_2~\lambda_3=1. Hence \lambda_2^2=\lambda_3^2=1/\lambda. Therefore,

I_1 = \lambda_1^2+\lambda_2^2+\lambda_3^2 = \lambda^2 + \cfrac{2}{\lambda} ~.

The left Cauchy-Green deformation tensor can then be expressed as

\boldsymbol{B} = \lambda^2~\mathbf{n}_1\otimes\mathbf{n}_1 + \cfrac{1}{\lambda}~(\mathbf{n}_2\otimes\mathbf{n}_2+\mathbf{n}_3\otimes\mathbf{n}_3) ~.

If the directions of the principal stretches are oriented with the coordinate basis vectors, we have

\sigma_{11} = -p + 2~\lambda^2~\cfrac{\partial W}{\partial I_1} ~;~~ \sigma_{22} = -p + \cfrac{2}{\lambda}~\cfrac{\partial W}{\partial I_1} = \sigma_{33} ~.

Since \sigma_{22} = \sigma_{33} = 0, we have

p = \cfrac{2}{\lambda}~\cfrac{\partial W}{\partial I_1} ~.

Therefore,

\sigma_{11} = 2~\left(\lambda^2 - \cfrac{1}{\lambda}\right)~\cfrac{\partial W}{\partial I_1}~.

The engineering strain is 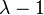\lambda-1\,. The engineering stress is

T_{11} = \sigma_{11}/\lambda = 2~\left(\lambda - \cfrac{1}{\lambda^2}\right)~\cfrac{\partial W}{\partial I_1}~.

Equibiaxial extension

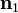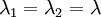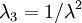For equibiaxial extension in the \mathbf{n}_1 and \mathbf{n}_2 directions, the principal stretches are \lambda_1 = \lambda_2 = \lambda\,. From incompressibility \lambda_1~\lambda_2~\lambda_3=1. Hence \lambda_3=1/\lambda^2\,. Therefore,

I_1 = \lambda_1^2+\lambda_2^2+\lambda_3^2 = 2~\lambda^2 + \cfrac{1}{\lambda^4} ~.

The left Cauchy-Green deformation tensor can then be expressed as

\boldsymbol{B} = \lambda^2~\mathbf{n}_1\otimes\mathbf{n}_1 + \lambda^2~\mathbf{n}_2\otimes\mathbf{n}_2+ \cfrac{1}{\lambda^4}~\mathbf{n}_3\otimes\mathbf{n}_3 ~.

If the directions of the principal stretches are oriented with the coordinate basis vectors, we have

\sigma_{11} = -p + 2~\lambda^2~\cfrac{\partial W}{\partial I_1} = \sigma_{22} ~;~~ \sigma_{33} = -p + \cfrac{2}{\lambda^4}~\cfrac{\partial W}{\partial I_1} ~.

Since \sigma_{33} = 0, we have

p = \cfrac{2}{\lambda^4}~\cfrac{\partial W}{\partial I_1} ~.

Therefore,

\sigma_{11} = 2~\left(\lambda^2 - \cfrac{1}{\lambda^4}\right)~\cfrac{\partial W}{\partial I_1} = \sigma_{22} ~.

The engineering strain is 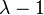\lambda-1\,. The engineering stress is

T_{11} = \cfrac{\sigma_{11}}{\lambda} = 2~\left(\lambda - \cfrac{1}{\lambda^5}\right)~\cfrac{\partial W}{\partial I_1} = T_{22}~.

Planar extension

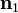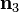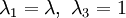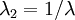Planar extension tests are carried out on thin specimens which are constrained from deforming in one direction. For planar extension in the \mathbf{n}_1 directions with the \mathbf{n}_3 direction constrained, the principal stretches are \lambda_1=\lambda, ~\lambda_3=1. From incompressibility \lambda_1~\lambda_2~\lambda_3=1. Hence \lambda_2=1/\lambda\,. Therefore,

I_1 = \lambda_1^2+\lambda_2^2+\lambda_3^2 = \lambda^2 + \cfrac{1}{\lambda^2} + 1 ~.

The left Cauchy-Green deformation tensor can then be expressed as

\boldsymbol{B} = \lambda^2~\mathbf{n}_1\otimes\mathbf{n}_1 + \cfrac{1}{\lambda^2}~\mathbf{n}_2\otimes\mathbf{n}_2+ \mathbf{n}_3\otimes\mathbf{n}_3 ~.

If the directions of the principal stretches are oriented with the coordinate basis vectors, we have

\sigma_{11} = -p + 2~\lambda^2~\cfrac{\partial W}{\partial I_1} ~;~~ \sigma_{22} = -p + \cfrac{2}{\lambda^2}~\cfrac{\partial W}{\partial I_1} ~;~~ \sigma_{33} = -p + 2~\cfrac{\partial W}{\partial I_1} ~.

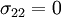Since \sigma_{22} = 0, we have

p = \cfrac{2}{\lambda^2}~\cfrac{\partial W}{\partial I_1} ~.

Therefore,

\sigma_{11} = 2~\left(\lambda^2 - \cfrac{1}{\lambda^2}\right)~\cfrac{\partial W}{\partial I_1} ~;~~ \sigma_{22} = 0 ~;~~ \sigma_{33} = 2~\left(1 - \cfrac{1}{\lambda^2}\right)~\cfrac{\partial W}{\partial I_1}~.

The engineering strain is 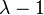\lambda-1\,. The engineering stress is

T_{11} = \cfrac{\sigma_{11}}{\lambda} = 2~\left(\lambda - \cfrac{1}{\lambda^3}\right)~\cfrac{\partial W}{\partial I_1}~.

Yeoh model for compressible rubbers

A version of the Yeoh model that includes 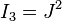I_3 = J^2 dependence is used for compressible rubbers. The strain energy density function for this model is written as

W = \sum_{i=1}^n C_{i0}~(\bar{I}_1-3)^i + \sum_{k=1}^n C_{k1}~(J-1)^{2k}

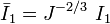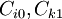where \bar{I}_1 = J^{-2/3}~I_1, and C_{i0}, C_{k1} are material constants. The quantity 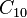C_{10} is interpreted as half the initial shear modulus, while 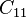C_{11} is interpreted as half the initial bulk modulus.

When n=1 the compressible Yeoh model reduces to the neo-Hookean model for incompressible materials.

References

  1. ↑ Yeoh, O. H., 1993, "Some forms of the strain energy function for rubber," Rubber Chemistry and technology, Volume 66, Issue 5, November 1993, Pages 754-771.
  2. ↑ Rivlin, R. S., 1948, "Some applications of elasticity theory to rubber engineering", in Collected Papers of R. S. Rivlin vol. 1 and 2, Springer, 1997.
  3. ↑ Selvadurai, A. P. S., 2006, "Deflections of a rubber membrane", Journal of the Mechanics and Physics of Solids, vol. 54, no. 6, pp. 1093-1119.

See also

This article is issued from Wikipedia - version of the 5/7/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.