Absolutely convex set

A set C in a real or complex vector space is said to be absolutely convex or disked if it is convex and balanced (circled), in which case it is called a disk.

Properties

A set $C$ is absolutely convex if and only if for any points $x_{1},\,x_{2}$ in $C$ and any numbers $\lambda _{1},\,\lambda _{2}$ satisfying $|\lambda _{1}|+|\lambda _{2}|\leq 1$ the sum $\lambda _{1}x_{1}+\lambda _{2}x_{2}$ belongs to $C$ .

Since the intersection of any collection of absolutely convex sets is absolutely convex then for any subset A of a vector space one can define its absolutely convex hull to be the intersection of all absolutely convex sets containing A.

Absolutely convex hull

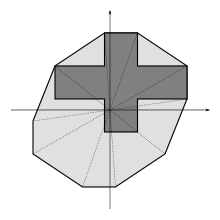
The light gray area is the Absolutely convex hull of the cross.

The absolutely convex hull of the set A assumes the following representation

${\mbox{absconv}}A=\left\{\sum _{{i=1}}^{n}\lambda _{i}x_{i}:n\in \mathbb{N} ,\,x_{i}\in A,\,\sum _{{i=1}}^{n}|\lambda _{i}|\leq 1\right\}$ .

References

Robertson, A.P.; W.J. Robertson (1964). Topological vector spaces. Cambridge Tracts in Mathematics. 53. Cambridge University Press. pp. 4–6.
Narici, Lawrence; Beckenstein, Edward (July 26, 2010). Topological Vector Spaces, Second Edition. Pure and Applied Mathematics (Second ed.). Chapman and Hall/CRC.

Schaefer, H.H. (1999). Topological vector spaces. Springer-Verlag Press. p. 39.

Functional analysis

Set / subset types	Absolutely convex Absorbing Balanced Bounded Convex Radial Star-shaped Symmetric Linear cone (subset) Convex cone (subset)

TVS types	Banach Barrelled Bornological Brauner F-space Finite-dimensional Fréchet (tame) Hilbert LF-space Locally convex Mackey Montel Nuclear Normed (norm) Quasinormed Reflexive Riesz Smith Stereotype Webbed Topological tensor product (of Hilbert spaces)

Mapping topologies	Dual Dual space Operator Ultraweak Weak (operator) Mackey Strong (polar operator) Ultrastrong Uniform convergence

Linear operators	Adjoint Bilinear (form) Bounded / Unbounded Closed Continuous / Discontinuous Compact Fredholm Hilbert–Schmidt Functionals (positive) Normal Nuclear Self-adjoint Strictly singular Trace class Transpose Unitary

Set operations	Algebraic interior (core) Interior Minkowski addition Polar

Operator theory	Banach algebras C-algebras Spectrum (C-algebra radius) Spectral theory (of ODEs Spectral theorem) Polar decomposition Singular value decomposition

Theorems	Banach–Alaoglu Banach–Saks Banach–Mazur Bessel's inequality Cauchy–Schwarz inequality Closed range Closed graph Eberlein–Šmulian Freudenthal spectral Gelfand–Mazur Goldstine Hahn–Banach (hyperplane separation) Kakutani fixed-point Lomonosov's invariant subspace Mackey–Arens Mazur's lemma M. Riesz extension Open mapping Parseval's identity Schauder fixed-point

Analysis	Bochner space Differentiation in Fréchet spaces Derivatives (Fréchet Gâteaux functional holomorphic) Integrals (Bochner Dunford Gelfand–Pettis regulated weak) Functional calculus (Borel continuous holomorphic) Inverse function theorem (Nash–Moser theorem) Vector measure Weakly measurable function

This article is issued from Wikipedia - version of the 9/25/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Absolutely convex set

Properties

Absolutely convex hull

See also

References