Analogical modeling

Linguistics
Theoretical
Cognitive Constraint-based Generative Structuralist Quantitative Functional theories of grammar Phonology Morphology Morphophonology Syntax Lexis Semantics Pragmatics Graphemics Orthography Semiotics
Descriptive
Anthropological Comparative Historical Etymology Graphetics Phonetics Sociolinguistics Cherology
Applied and experimental
Computational Contrastive Evolutionary Forensic Internet Language acquisition Second-language acquisition Language assessment Language development Language education Linguistic anthropology Neurolinguistics Psycholinguistics
Related articles
History of linguistics Linguistic prescription List of linguists Unsolved linguistics problems
Linguistics portal

Analogical modeling (hereafter AM) is a formal theory of exemplar based analogical reasoning, proposed by Royal Skousen, professor of Linguistics and English language at Brigham Young University in Provo, Utah. It is applicable to language modeling and other categorization tasks. Analogical modeling is related to connectionism and nearest neighbor approaches, in that it is data-based rather than abstraction-based; but it is distinguished by its ability to cope with imperfect datasets (such as caused by simulated short term memory limits) and to base predictions on all relevant segments of the dataset, whether near or far. In language modeling, AM has successfully predicted empirically valid forms for which no theoretical explanation was known (see the discussion of Finnish morphology in Skousen et al. 2002).

Implementation of the model

Overview

An exemplar-based model consists of a general-purpose modeling engine and a problem-specific dataset. Within the dataset, each exemplar (a case to be reasoned from, or an informative past experience) appears as a feature vector: a row of values for parameters that describe the problem. For example, in a spelling-to-sound task, the feature vector might consist of the letters of a word. Each exemplar in the dataset is stored with an outcome, such as a phoneme or phone to be generated. When the model is presented with a novel situation (in the form of an outcome-less feature vector), the engine algorithmically sorts the dataset to find exemplars that helpfully resemble it, and selects one, whose outcome is the model's prediction. The particulars of this algorithm distinguish one exemplar-based modeling system from another.

In AM, we think of the feature values as characterizing a context, and the outcome as a behavior that occurs within that context. Accordingly, the novel situation is known as the given context. Given the known features of the context, the AM engine systematically generates all contexts that include it (all of its supracontexts), and extracts from the dataset the exemplars that belong to each. The engine then discards those supracontexts whose outcomes are inconsistent (this measure of consistency will be discussed further below), leaving an analogical set of supracontexts, and probabilistically selects an exemplar from the analogical set with a bias toward those in large supracontexts. This multilevel search exponentially magnifies the likelihood of a behavior's being predicted as it occurs reliably in settings that specifically resemble the given context.

Analogical modeling in detail

AM performs the same process for each case it is asked to evaluate. The given context, consisting of n variables, is used as a template to generate two-to-the-n supracontexts. Each supracontext is a set of exemplars in which one or more variables have the same values that they do in the given context, and the other variables are ignored. In effect, each is a view of the data, created by filtering for some criteria of similarity to the given context, and the total set of supracontexts exhausts all such views. Alternatively, each supracontext is a theory of the task or a proposed rule whose predictive power needs to be evaluated.

It is important to note that the supracontexts are not equal peers one with another; they are arranged by their distance from the given context, forming a hierarchy. If a supracontext specifies all of the variables that another one does and more, it is a subcontext of that other one, and it lies closer to the given context. (The hierarchy is not strictly branching; each supracontext can itself be a subcontext of several others, and can have several subcontexts.) This hierarchy becomes significant in the next step of the algorithm.

The engine now chooses the analogical set from among the supracontexts. A supracontext may contain exemplars that only exhibit one behavior; it is deterministically homogeneous and is included. It is a view of the data that displays regularity, or a relevant theory that has never yet been disproven. A supracontext may exhibit several behaviors, but contain no exemplars that occur in any more specific supracontext (that is, in any of its subcontexts); in this case it is non-deterministically homogeneous and is included. Here there is no great evidence that a systematic behavior occurs, but also no counterargument. Finally, a supracontext may be heterogeneous, meaning that it exhibits behaviors that are found in a subcontext (closer to the given context), and also behaviors that are not. Where the ambiguous behavior of the nondeterministically homogeneous supracontext was accepted, this is rejected because the intervening subcontext demonstrates that there is a better theory to be found. The heterogeneous supracontext is therefore excluded. This guarantees that we see an increase in meaningfully consistent behavior in the analogical set as we approach the given context.

With the analogical set chosen, each appearance of an exemplar (for a given exemplar may appear in several of the analogical supracontexts) is given a pointer to every other appearance of an exemplar within its supracontexts. One of these pointers is then selected at random and followed, and the exemplar to which it points provides the outcome. This gives each supracontext an importance proportional to the square of its size, and makes each exemplar likely to be selected in direct proportion to the sum of the sizes of all analogically consistent supracontexts in which it appears. Then, of course, the probability of predicting a particular outcome is proportional to the summed probabilities of all the exemplars that support it.

(Skousen 2002, in Skousen et al. 2002, pp. 11–25, and Skousen 2003, both passim)

Formulas

Given a context with $n$ elements:

total number of pairings:

n^{2}

number of agreements for outcome i:

n_{i}^{2}

number of disagreements for outcome i:

n_{i}(n-n_{i})

total number of agreements:

\sum {n_{i}^{2}}

total number of disagreements:

\sum {n_{i}(n-n_{i})}=n^{2}-\sum {n_{i}^{2}}

Example

This terminology is best understood through an example. In the example used in the second chapter of Skousen (1989), each context consists of three variables with potential values 0-3

Variable 1: 0,1,2,3

Variable 2: 0,1,2,3

Variable 3: 0,1,2,3

The two outcomes for the dataset are e and r, and the exemplars are:

3 1 0 e

0 3 2 r

2 1 0 r

2 1 2 r

3 1 1 r

We define a network of pointers like so:

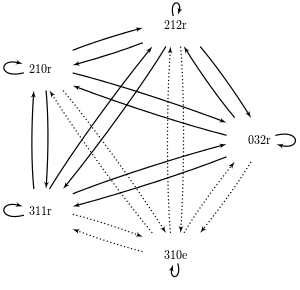
The solid lines represent pointers between exemplars with matching outcomes; the dotted lines represent pointers between exemplars with non-matching outcomes.

The statistics for this example are as follows:

n=5

n_{r}=4

n_{e}=1

total number of pairings:

n^{2}=25

number of agreements for outcome r:

n_{r}^{2}=16

number of agreements for outcome e:

n_{e}^{2}=1

number of disagreements for outcome r:

n_{r}(n-n_{r})=4

number of disagreements for outcome e:

n_{e}(n-n_{e})=4

total number of agreements:

n_{r}^{2}+n_{e}^{2}=17

total number of disagreements:

n_{r}(n-n_{r})+n_{e}(n-n_{e})=n^{2}-(n_{r}^{2}+n_{e}^{2})=8

uncertainty or fraction of disagreement:

8/25=.32

Behavior can only be predicted for a given context; in this example, let us predict the outcome for the context "3 1 2". To do this, we first find all of the contexts containing the given context; these contexts are called supracontexts. We find the supracontexts by systematically eliminating the variables in the given context; with m variables, there will generally be $2^{m}$ supracontexts. The following table lists each of the sub- and supracontexts; x means "not x", and - means "anything".

Supracontext	Subcontexts
3 1 2	3 1 2
3 1 -	3 1 2, 3 1 2
3 - 2	3 1 2, 3 1 2
- 1 2	3 1 2, 3 1 2
3 - -	3 1 2, 3 1 2, 3 1 2, 3 1 2
- 1 -	3 1 2, 3 1 2, 3 1 2, 3 1 2
- - 2	3 1 2, 3 1 2, 3 1 2, 3 1 2
- - -	3 1 2, 3 1 2, 3 1 2, 3 1 2, 3 1 2, 3 1 2, 3 1 2, 3 1 2

These contexts are shown in the venn diagram below:

The next step is to determine which exemplars belong to which contexts in order to determine which of the contexts are homogeneous. The table below shows each of the subcontexts, their behavior in terms of the given exemplars, and the number of disagreements within the behavior:

Subcontext	Behavior	Disagreements
3 1 2	(empty)	0
3 1 2	3 1 0 e, 3 1 1 r	2
3 1 2	(empty)	0
3 1 2	2 1 2 r	0
3 1 2	(empty)	0
3 1 2	2 1 0 r	0
3 1 2	0 3 2 r	0
31 2	(empty)	0

Analyzing the subcontexts in the table above, we see that there is only 1 subcontext with any disagreements: "3 1 2", which in the dataset consists of "3 1 0 e" and "3 1 1 r". There are 2 disagreements in this subcontext; 1 pointing from each of the exemplars to the other (see the pointer network pictured above). Therefore, only supracontexts containing this subcontext will contain any disagreements. We use a simple rule to identify the homogeneous supracontexts:

If the number if disagreements in the supracontext is greater than the number of disagreements in the contained subcontext, we say that it is heterogeneous; otherwise, it is homogeneous.

There are 3 situations that produce a homogeneous supracontext:

The supracontext is empty. This is the case for "3 - 2", which contains no data points. There can be no increase in the number of disagreements, and the supracontext is trivially homogeneous.
The supracontext is deterministic, meaning that only one type of outcome occurs in it. This is the case for "- 1 2" and "- - 2", which contain only data with the r outcome.
Only one subcontext contains any data. The subcontext does not have to be deterministic for the supracontext to be homogeneous. For example, while the supracontexts "3 1 -" and "- 1 2" are deterministic and only contain one non-empty subcontext, "3 - -" contains only the subcontext "3 1 2". This subcontext contains "3 1 0 e" and "3 1 1 r", making it non-deterministic. We say that this type of supracontext is unobstructed and non-deterministic.

The only two heterogeneous supracontexts are "- 1 -" and "- - -". In both of them, it is the combination of the non-deterministic "3 1 2" with other subcontexts containing the r outcome which causes the heterogeneity.

There is actually a 4th type of homogeneous supracontext: it contains more than one non-empty subcontext and it is non-deterministic, but the frequency of outcomes in each sub-context is exactly the same. Analogical modeling does not consider this situation, however, for 2 reasons:

Determining whether this 4 situation has occurred requires a $\chi ^{2}$ test. This is the only test of homogeneity that requires arithmetic, and ignoring it allows our tests of homogeneity to become statistically free, which makes AM better for modeling human reasoning.
It is an extremely rare situation, and thus ignoring it will can be expected not to have a large effect on the predicted outcome.

Next we construct the analogical set, which consists of all of the pointers and outcomes from the homogeneous supracontexts. The figure below shows the pointer network with the homogeneous contexts highlighted.

The pointers are summarized in the following table:

Homogeneous
supracontext

Occurrences

Number of
pointers

e	r

3 1 -

"3 1 0 e", "3 1 1 r"

- 1 2

"2 1 2 r"

3 - -

"3 1 0 e", "3 1 1 r"

- - 2

"2 1 2 r", "0 3 2 r"

Totals:

4 of the pointers in the analogical set are associated with the outcome e, and the other 9 are associated with r. In AM, a pointer is randomly selected and the outcome it points to is predicted. With a total of 13 pointers, the probability of the outcome e being predicted is 4/13 or 30.8%, and for outcome r it is 9/13 or 69.2%. We can create a more detailed account by listing the pointers for each of the occurrences in the homogeneous supracontexts:

Occurrence	Number of homogeneous supracontexts	Number of pointers	Analogical effect
3 1 0 e	2	4	30.8%
3 1 1 r	2	4	30.8%
2 1 2 r	2	3	23.1%
0 3 2 r	1	2	15.4%
2 1 0 r	0	0	0.0%

We can then see the analogical effect of each of the instances in the data set.

Historical Context

Analogy has been considered useful in describing language at least since the time of Saussure. Noam Chomsky and others have more recently criticized analogy as too vague to really be useful (Bańko 1991), an appeal to a deus ex machina. Skousen's proposal appears to address that criticism by proposing an explicit mechanism for analogy, which can be tested for psychological validity.

Applications

Analogical modeling has been employed in experiments ranging from phonology and morphology (linguistics) to orthography and syntax.

Problems

Though analogical modeling aims to create a model free from rules seen as contrived by linguists, in its current form it still requires researchers to select which variables to take into consideration. This is necessary because of the so-called "exponential explosion" of processing power requirements of the computer software used to implement analogical modeling. Recent research suggests that quantum computing could provide the solution to such performance bottlenecks (Skousen et al. 2002, see pp 45–47).

References

Royal Skousen (1989). Analogical Modeling of Language (hardcover). Dordrecht: Kluwer Academic Publishers. xii+212pp. ISBN 0-7923-0517-5.
Miroslaw Bańko (June 1991). "Review: Analogical Modeling of Language" (PDF). Computational Linguistics. 17 (2): 246–248.
Royal Skousen (1992). Analogy and Structure. Dordrect: Kluwer Academic Publishers. ISBN 0-7923-1935-4.
Royal Skousen; Deryle Lonsdale; Dilworth B. Parkinson, eds. (2002). Analogical Modeling: An exemplar-based approach to language (Human Cognitive Processing vol. 10). Amsterdam/Philadelphia: John Benjamins Publishing Company. p. x+417pp. ISBN 1-58811-302-7.
Skousen, Royal. (2003). Analogical Modeling: Exemplars, Rules, and Quantum Computing. Presented at the Berkeley Linguistics Society conference.

External links

Analogical Modeling Research Group Homepage
LINGUIST List Announcement of Analogical Modeling, Skousen et al. (2002)

This article is issued from Wikipedia - version of the 6/8/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.