Aztec diamond
In combinatorial mathematics, an Aztec diamond of order n consists of all squares of a square lattice whose centers (x,y) satisfy |x| + |y| ≤ n. Here n is a fixed integer, and the square lattice consists of unit squares with the origin as a vertex of 4 of them, so that both x and y are half-integers.[1]
The Aztec diamond theorem states that the number of domino tilings of the Aztec diamond of order n is 2n(n+1)/2.[2] The arctic circle theorem says that a random tiling of a large Aztec diamond tends to be frozen outside a certain circle.[3]
-

An Aztec diamond of order 4, with 1024 domino tilings
-
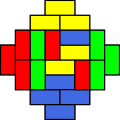
One possible tiling.
-

A tiling of a hexagon chosen uniformly at random, with the "frozen" tiles being depicted in white. (Arctic Circle theorem.)
It is common to color the tiles in the following fashion. First consider a checkerboard coloring of the diamond. Each tile will cover exactly one black square. Vertical tiles where the top square covers a black square, is colored in one color, and the other vertical tiles in a second. Similarly for horizontal tiles.
References
- ↑ Stanley, Richard P. (1999), Enumerative combinatorics. Vol. 2, Cambridge Studies in Advanced Mathematics, 62, Cambridge University Press, ISBN 978-0-521-56069-6, MR 1676282
- ↑ Elkies, Noam; Kuperberg, Greg; Larsen, Michael; Propp, James (1992), "Alternating-sign matrices and domino tilings. I", Journal of Algebraic Combinatorics. An International Journal, 1 (2): 111–132, doi:10.1023/A:1022420103267, ISSN 0925-9899, MR 1226347
- ↑ Jockusch, William; Propp, James; Shor, Peter (1998), Random Domino Tilings and the Arctic Circle Theorem