Diagrammatic reasoning

Diagrammatic reasoning is reasoning by means of visual representations. The study of diagrammatic reasoning is about the understanding of concepts and ideas, visualized with the use of diagrams and imagery instead of by linguistic or algebraic means.

Characteristica universalis, commonly interpreted as universal characteristic, or universal character in English, is a universal and formal language imagined by the German philosopher Gottfried Leibniz able to express mathematical, scientific, and metaphysical concepts. Leibniz thus hoped to create a language usable within the framework of a universal logical calculation or calculus ratiocinator.

Leibniz's diagrammatic reasoning.

Since the characteristica universalis is diagrammatic and employs pictograms (below left), the diagrams in Leibniz's work warrant close study. On at least two occasions, Leibniz illustrated his philosophical reasoning with diagrams. One diagram, the frontispiece to his 1666 De Arte Combinatoria (On the Art of Combinations), represents the Aristotelian theory of how all material things are formed from combinations of the elements earth, water, air, and fire.

Basic elements of Leibniz's pictograms.

These four elements make up the four corners of a diamond (see picture to right). Opposing pairs of these are joined by a bar labeled "contraries" (earth-air, fire-water). At the four corners of the superimposed square are the four qualities defining the elements. Each adjacent pair of these is joined by a bar labeled "possible combination"; the diagonals joining them are labeled "impossible combination." Starting from the top, fire is formed from the combination of dryness and heat; air from wetness and heat; water from coldness and wetness; earth from coldness and dryness.^[1]

Diagram

A diagram is a 2D geometric symbolic representation of information according to some visualization technique. Sometimes, the technique uses a 3D visualization which is then projected onto the 2D surface. The term diagram in common sense can have two meanings.

Sample flowchart representing the decision process to add a new article to Wikipedia.

visual information device: Like the term "illustration" the diagram is used as a collective term standing for the whole class of technical genres, including graphs, technical drawings and tables.^[2]
specific kind of visual display: This is only the genre, that shows qualitative data with shapes that are connected by lines, arrows, or other visual links.

In science you will find the term used in both ways. For example, Anderson (1997) stated more general "diagrams are pictorial, yet abstract, representations of information, and maps, line graphs, bar charts, engineering blueprints, and architects' sketches are all examples of diagrams, whereas photographs and video are not".^[3] On the other hand, Lowe (1993) defined diagrams as specifically "abstract graphic portrayals of the subject matter they represent".^[4]

In the specific sense diagrams and charts contrast computer graphics, technical illustrations, infographics, maps, and technical drawings, by showing "abstract rather than literal representations of information".^[2] The essences of a diagram can be seen as:^[2]

a form of visual formatting devices
a display that does not show quantitative data, but rather relationships and abstract information
with building blocks such as geometrical shapes that are connected by lines, arrows, or other visual links.

Or as Bert S. Hall wrote, "diagrams are simplified figures, caricatures in a way, intended to convey essential meaning".^[5] According to Jan V. White (1984) "the characteristics of a good diagram are elegance, clarity, ease, pattern, simplicity, and validity".^[2] Elegance for White means that what you are seeing in the diagram is "the simplest and most fitting solution to a problem".^[6]

Logical graph

A logical graph is a special type of graph-theoretic structure in any one of several systems of graphical syntax that Charles Sanders Peirce developed for logic.

In his papers on qualitative logic, entitative graphs, and existential graphs, Peirce developed several versions of a graphical formalism, or a graph-theoretic formal language, designed to be interpreted for logic.

In the century since Peirce initiated this line of development, a variety of formal systems have branched out from what is abstractly the same formal base of graph-theoretic structures.

Conceptual graph

A conceptual graph (CG) is a notation for logic based on the existential graphs of Charles Sanders Peirce and the semantic networks of artificial intelligence. In the first published paper on conceptual graphs, John F. Sowa used them to represent the conceptual schemas used in database systems. His first book^[7] applied them to a wide range of topics in artificial intelligence, computer science, and cognitive science. A linear notation, called the Conceptual Graph Interchange Format (CGIF), has been standardized in the ISO standard for Common Logic.

Elsie the cat is sitting on a mat

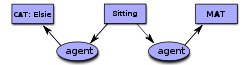
The diagram on the right is an example of the display form for a conceptual graph. Each box is called a concept node, and each oval is called a relation node. In CGIF, this CG would be represented by the following statement:

[Cat Elsie] [Sitting *x] [Mat *y] (agent ?x Elsie) (location ?x ?y)

In CGIF, brackets enclose the information inside the concept nodes, and parentheses enclose the information inside the relation nodes. The letters x and y, which are called coreference labels, show how the concept and relation nodes are connected. In the Common Logic Interchange Format (CLIF), those letters are mapped to variables, as in the following statement:

(exists ((x Sitting) (y Mat)) (and (Cat Elsie) (agent x Elsie) (location x y)))

As this example shows, the asterisks on the coreference labels *x and *y in CGIF map to existentially quantified variables in CLIF, and the question marks on ?x and ?y map to bound variables in CLIF. A universal quantifier, represented @every*z in CGIF, would be represented forall (z) in CLIF.

Entitative graph

An entitative graph is an element of the graphical syntax for logic that Charles Sanders Peirce developed under the name of qualitative logic beginning in the 1880s, taking the coverage of the formalism only as far as the propositional or sentential aspects of logic are concerned.^[8]

The syntax is:

The blank page;
Single letters, phrases;
Objects (subgraphs) enclosed by a simple closed curve called a cut. A cut can be empty.

The semantics are:

The blank page denotes False;
Letters, phrases, subgraphs, and entire graphs can be True' or False;
To surround objects with a cut is equivalent to Boolean complementation. Hence an empty cut denotes Truth;
All objects within a given cut are tacitly joined by disjunction.

A "proof" manipulates a graph, using a short list of rules, until the graph is reduced to an empty cut or the blank page. A graph that can be so reduced is what is now called a tautology (or the complement thereof). Graphs that cannot be simplified beyond a certain point are analogues of the satisfiable formulas of first-order logic.

Existential graph

An existential graph is a type of diagrammatic or visual notation for logical expressions, proposed by Charles Sanders Peirce, who wrote his first paper on graphical logic in 1882 and continued to develop the method until his death in 1914. Peirce proposed three systems of existential graphs:

alpha – isomorphic to sentential logic and the two-element Boolean algebra;
beta – isomorphic to first-order logic with identity, with all formulas closed;
gamma – (nearly) isomorphic to normal modal logic.

Alpha nests in beta and gamma. Beta does not nest in gamma, quantified modal logic being more than even Peirce could envisage.

Alpha Graphs

In alpha the syntax is:

The blank page;
Single letters or phrases written anywhere on the page;
Any graph may be enclosed by a simple closed curve called a cut or sep. A cut can be empty. Cuts can nest and concatenate at will, but must never intersect.

Any well-formed part of a graph is a subgraph.

The semantics are:

The blank page denotes Truth;
Letters, phrases, subgraphs, and entire graphs may be True or False;
To enclose a subgraph with a cut is equivalent to logical negation or Boolean complementation. Hence an empty cut denotes False;
All subgraphs within a given cut are tacitly conjoined.

Hence the alpha graphs are a minimalist notation for sentential logic, grounded in the expressive adequacy of And and Not. The alpha graphs constitute a radical simplification of the two-element Boolean algebra and the truth functors.

The Venn-II reasoning system

In the early 1990s Sun-Joo Shin presented an extension of Existential Graphs called Venn-II.^[9] Syntax and semantics are given formally, together with a set of Rules of Transformation which are shown to be sound and complete. Proofs proceed by applying the rules (which remove or add syntactic elements to or from diagrams) sequentially. Venn-II is equivalent in expressive power to a first-order monadic language.

References

↑ This diagram is reproduced in several texts including Saemtliche Schriften und Briefe, Reihe VI, Band 1: 166, Loemker 1969: 83, 366, Karl Popp and Erwin Stein 2000: 33.
1 2 3 4 Brasseur, Lee E. (2003). Visualizing technical information: a cultural critique. Amityville, N.Y.: Baywood Pub. ISBN 0-89503-240-6.
↑ Michael Anderson (1997). "Introduction to Diagrammatic Reasoning". Retrieved 21 July 2008.
↑ Lowe, Richard K. (1993). "Diagrammatic information: techniques for exploring its mental representation and processing". Information Design Journal. 7 (1): 3–18. doi:10.1075/idj.7.1.01low.
↑ Bert S. Hall (1996). "The Didactic and the Elegant: Some Thoughts on Scientific and Technological Illustrations in the Middle Ages and Renaissance". in: B. Braigie (ed.) Picturing knowledge: historical and philosophical problems concerning the use of art in science. Toronto: University of Toronto Press. p.9
↑ White, Jan V. (1984). Using charts and graphs: 1000 ideas for visual persuasion. New York: Bowker. ISBN 0-8352-1894-5.
↑ John F. Sowa (1984). Conceptual Structures: Information Processing in Mind and Machine. Addison-Wesley, Reading, MA, 1984.
↑ See 3.468, 4.434, and 4.564 in Peirce's Collected Papers.
↑ Shin, Sun-Joo. 1994. The Logical Status of Diagrams. Cambridge: Cambridge University Press.

External links

Diagrammatic Reasoning Site from the University of Hartford,Connecticut, USA
Lecture about Universal Algebra and Diagrammatic Reasoning by John Baez, 3 Feb 2006.
Homepage of Sun-Joo Shin.
Visual Modelling Group at the University of Brighton, UK.

This article is issued from Wikipedia - version of the 10/8/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.