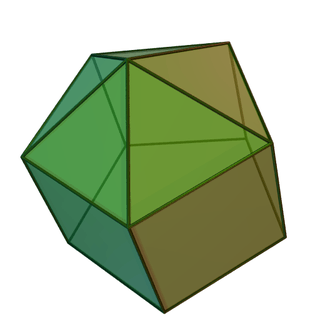
Elongated pentagonal pyramid
| Elongated pentagonal pyramid | |
|---|---|
 | |
| Type |
Johnson J8 - J9 - J10 |
| Faces |
5 triangles 5 squares 1 pentagon |
| Edges | 20 |
| Vertices | 11 |
| Vertex configuration |
5(42.5) 5(32.42) |
| Symmetry group | C5v, [5], (*55) |
| Rotation group | C5, [5]+, (55) |
| Dual polyhedron | self |
| Properties | convex |
| Net | |
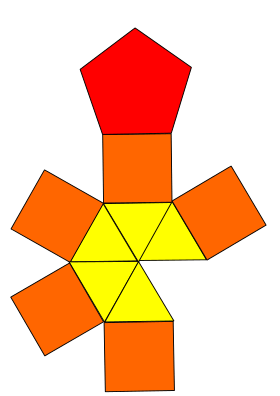 | |
In geometry, the elongated pentagonal pyramid is one of the Johnson solids (J9). As the name suggests, it can be constructed by elongating a pentagonal pyramid (J2) by attaching a pentagonal prism to its base.
A Johnson solid is one of 92 strictly convex polyhedra that have regular faces but are not uniform (that is, they are not Platonic solids, Archimedean solids, prisms or antiprisms). They were named by Norman Johnson, who first listed these polyhedra in 1966.[1]
Dual polyhedron
The dual of the elongated pentagonal pyramid has 11 faces: 5 triangular, 1 pentagonal and 5 trapezoidal.
| Dual elongated pentagonal pyramid | Net of dual |
|---|---|
 |
 |
See also
External links
- ↑ Johnson, Norman W. (1966), "Convex polyhedra with regular faces", Canadian Journal of Mathematics, 18: 169–200, doi:10.4153/cjm-1966-021-8, MR 0185507, Zbl 0132.14603.
This article is issued from Wikipedia - version of the 11/5/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.
