Juggling notation

Juggling notation is the written depiction of concepts and practices in juggling.[1][2] Toss juggling patterns have a reputation for being "easier done than said" – while it might be easy to learn a given maneuver and demonstrate it for others, it is often much harder to communicate the idea accurately using speech or plain text. To circumvent this problem, various numeric or diagram-based notation systems have been developed to facilitate communication of patterns or tricks between jugglers, as well the investigation and discovery of new patterns.
A juggling notation system (based on music notation) was first proposed by Dave Storer in 1978 and while the first juggling diagram (a ladder diagram), by Claude Shannon around 1981, was not printed till 2010, the first printed diagram and second oldest notation system were proposed by Jeff Walker in 1982.[3]
Diagram-based
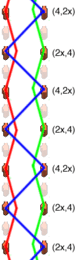
3-ball box
While diagrams are the most visual and reader-friendly way to notate many juggling patterns, they rely on images, so are complicated to produce and unwieldy to share via text or speech.
- Ladder diagrams - Each rung on the "ladder" represents a point in time (or "beat"). The juggled objects are represented as lines, their paths through time and between a pair of hands.
- Causal diagrams - Similar to the ladder diagram but doesn't show the props held in a juggler's hands. Instead it only shows each "problem" — an incoming prop — and what the juggler should do to make space in his or her hands to catch that incoming prop. It is usually used for club passing and can be displayed or edited in some juggling software.
- Mills Mess State Transition Diagrams - Mills Mess is a popular pattern in which the arms cross and uncross. Mills Mess State Transition Diagrams can be used to track these basic arm movements.
Numeric
The following notation systems use only numbers and common characters. The patterns can easily be communicated by text. Most numeric systems are designed to be processed by software juggling simulators — for example, to view juggling patterns as computer animations.
Siteswap
Developed by mathematically inclined jugglers Bengt Magnusson and Bruce Boppo Tiemann in 1985,[1][4][5] siteswap is by far the most common juggling notation.
A given juggling pattern is represented by a sequence of digits, like "333", "97531", or "744". Each digit represents the number of throws that occur by the time that same prop will be caught. For example, "333" represents a common three-ball cascade, where three props are thrown before the same prop will be caught and thrown again. Within the "531531" pattern, the prop thrown first, the '5' throw, will not be caught until five throws have been made, including itself, where it will be thrown again as a '1'. The prop thrown next, the '3', will be thrown again on the third throw afterwards, the next '3'. And the next prop is thrown with a '1' throw, which is a direct pass to the other hand and will be thrown on the very next throw as a '5'.
Because the number represents the number of throws that occur before that prop will be caught, it can be also be thought to describe how high one throws the prop, or how long it remains in the air relative to the other throws, where even numbers inevitably come back to the same hand and odd numbers cross over to the other hand.
The number of props in a given juggling pattern can be determined by the average of one repeating group. "633633633", therefore describes a four-prop pattern, while "414414414" describes a three-prop juggling pattern.
"Vanilla" siteswap is the most basic form of siteswap and uses only a simple string of digits to describe patterns that throw only one prop at a time, alternating between hands. For slightly more complicated patterns, extra rules and syntax are added to create the following two siteswap extensions:
- Synchronous Siteswap, or "Synch" Siteswap. This is used to notate patterns where both hands throw at the same time, rather than alternating left and right hands. The numbers for the two throws are combined in parentheses and separated by a comma. For example, "(4,4)(4,4)(4,4)".
- Multiplex Siteswap. "Multiplex", in the world of juggling, means "more than one ball is in the hand at the time of the throw". Multiplex Siteswap allows you to notate such patterns, and also can be mixed with synchronous siteswap. A multiplex is described by a digit for each prop in the multiplex throw contained within square brackets. "23[43]23[43]" is a common four ball multiplex.
Vanilla, synch, and multiplex siteswap are the "standard" forms of siteswap. Not only are they understood by jugglers, there are also many computer programs capable of animating juggling patterns entered in siteswap notation.
Other extensions to siteswap have been developed for specific purposes. These are far less common than the "standard" forms of siteswap, understood by far fewer jugglers and only specialized software.
- Passing siteswap - used for simple passing patterns.
- Multi-Hand Notation (MHN) - Developed by Ed Carstens for use with his juggling program JugglePro, MHN can describe patterns with any number of hands and at any rhythm, but use is limited due to its being as complex as a computer programming language.
- Generalized Siteswap (GS) - Developed by Ben Beever, GS places siteswap into a matrix that uses optional, additional rows to describe any desired attributes of the throws or catches within a pattern, such as timing issues (e.g. for synch patterns), number of spins (e.g. for clubs) and hand position/orientation (e.g. for backcrosses, claw catches etc.).[6]
References
- 1 2 Klarreich, Erica (December 25, 2004). "New juggling tricks created by maths". New Scientist (2479). Retrieved August 29, 2009.
- ↑ Beek, Peter J.; Lewbel, Arthur (November 1995). "The Science of Juggling" (PDF). Scientific American. 273 (5): 92–97. doi:10.1038/scientificamerican1195-92. Retrieved August 29, 2009.
- ↑ Lewbel, Arthur (1996). "The Academic Juggler: The Invention Of Juggling Notations", Juggle.org.
- ↑ Donahue, Bill (1996-04-16). "Jugglers Now Juggle Numbers to Compute New Tricks for Ancient Art". The New York Times. The New York Times Company. Retrieved August 29, 2009.
- ↑ "Read This: The Mathematics of Juggling". Mathematical Association of America. 2003-12-03. Retrieved August 29, 2009.
- ↑ Beever, Ben (20 January 2002). "SS Ben's Guide to Juggling Patterns" (PDF). The Juggling Edge. Retrieved 5 February 2010.
External links
- Juggling notation at DMOZ
- Juggling notation interactive graphic at Boston.com
