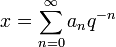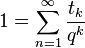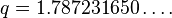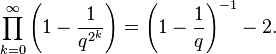Komornik–Loreti constant
The Komornik–Loreti constant is a mathematical constant that represents the smallest number for which there still exists a unique q-development.
Definition
Given a real number q > 1, the series
is called the q-expansion, or 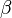 -expansion, of the positive real number x if, for all
-expansion, of the positive real number x if, for all 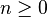 ,
, 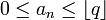 , where
, where 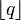 is the floor function and
is the floor function and 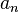 need not be an integer. Any real number
need not be an integer. Any real number 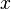 such that
such that 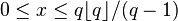 has such an expansion, as can be found using the greedy algorithm.
has such an expansion, as can be found using the greedy algorithm.
The special case of 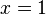 ,
, 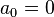 , and
, and 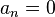 or 1 is sometimes called a
or 1 is sometimes called a 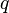 -development.
-development. 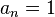 gives the only 2-development. However, for almost all
gives the only 2-development. However, for almost all 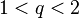 , there are an infinite number of different
, there are an infinite number of different 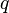 -developments. Even more surprisingly though, there exist exceptional
-developments. Even more surprisingly though, there exist exceptional 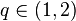 for which there exists only a single
for which there exists only a single 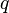 -development. Furthermore, there is a smallest number
-development. Furthermore, there is a smallest number 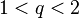 known as the Komornik–Loreti constant for which there exists a unique
known as the Komornik–Loreti constant for which there exists a unique 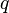 -development.[1]
-development.[1]
The Komornik–Loreti constant is the value 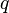 such that
such that
where 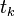 is the Thue–Morse sequence, i.e.,
is the Thue–Morse sequence, i.e., 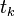 is the parity of the number of 1's in the binary representation of
is the parity of the number of 1's in the binary representation of 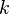 . It has approximate value
. It has approximate value
The constant 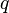 is also the unique positive real root of
is also the unique positive real root of
This constant is transcendental.[2]
References
- ↑ Weissman, Eric W. "q-expansion" From Wolfram MathWorld. Retrieved on 2009-10-18.
- ↑ Weissman, Eric W. "Komornik–Loreti Constant." From Wolfram MathWorld. Retrieved on 2010-12-27.