Meyer wavelet
The Meyer wavelet is an orthogonal wavelet proposed by Yves Meyer. It is infinitely differentiable with infinite support and defined in frequency domain in terms of function as:
where:
There are many different ways for defining this auxiliary function, which yields variants of the Meyer wavelet. For instance, another standard implementation adopts

Spectrum of the Meyer wavelet.
The Meyer scale function is given by:
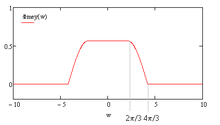
Meyer scale function.
In the time-domain, the waveform of the Meyer mother-wavelet has the shape as shown in the following figure:
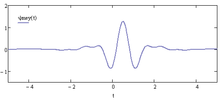
Meyer wavelet.
In 2015, Victor Vermehren Valenzuela and H. M. de Oliveira gave the explicitly expressions of Meyer wavelet and scale functions:
and
where
and
References
- Meyer (Y.), Ondelettes et Opérateurs, Hermann, 1990.
- Daubechies, (I.), Ten lectures on wavelets, CBMS-NSF conference series in applied mathematics, SIAM Ed., pp. 117–119, 137, 152, 1992.
- Victor Vermehren Valenzuela and H. M. de Oliveira, Close expressions for Meyer Wavelet and Scale Function, 2015, p.4.
External links
| Look up wavelet in Wiktionary, the free dictionary. |
| Wikimedia Commons has media related to Wavelet. |
This article is issued from Wikipedia - version of the 9/2/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.
