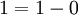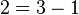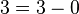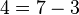Perfect ruler
A perfect ruler of length 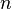 is a ruler with a subset of the integer markings
is a ruler with a subset of the integer markings 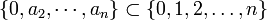 that appear on a regular ruler. The defining criterion of this subset is that there exists an
that appear on a regular ruler. The defining criterion of this subset is that there exists an 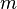 such that any positive integer
such that any positive integer 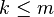 can be expressed uniquely as a difference
can be expressed uniquely as a difference 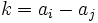 for some
for some 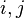 . This is referred to as an
. This is referred to as an 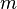 -perfect ruler.
-perfect ruler.
A 4-perfect ruler of length 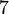 is given by
is given by  . To verify this, we need to show that every number
. To verify this, we need to show that every number  can be expressed as a difference of two numbers in the above set:
can be expressed as a difference of two numbers in the above set:
An optimal perfect ruler is one where for a fixed value of  the value of
the value of  is minimized.
is minimized.
See also
This article incorporates material from perfect ruler on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.
This article is issued from Wikipedia - version of the 3/18/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.